![]()
量子隐形传态(Quantum Teleportation)
本教程将带你了解量子信息领域一个广受欢迎的技术——量子隐形传态。虽然隐形传态常被认为是科幻小说中的内容,但我们将证明它在今天已经成为可能!这一技术利用了量子计算中许多基础原理,并在整个领域有广泛的应用。这些原理包括(但不限于):不可克隆定理、量子纠缠和延迟测量原理。让我们一探究竟吧!
目标:传输量子信息
假设有两位研究人员 Alice 和 Bob,Alice 想要将她的量子态发送给 Bob。量子隐形传态协议能够以一种非常优雅的方式实现这一点,整个过程可以分为四个步骤:
- 态制备:Alice 将她的量子比特初始化为她希望传送的状态。
-
共享纠缠:创建一个 Bell 态并分发给 Alice 和 Bob(每人一个量子比特)。
-
基矢变换:Alice 将她的两个量子比特从 Bell 基矢转换到计算基矢。
-
测量:Alice 测量她的两个量子比特,然后告诉 Bob 如何转换他的量子比特以获得期望的状态。请注意,传送的只是量子信息,而不是实际的粒子。
问题:不可克隆定理
你可能会想,为什么我们需要传送量子态呢?Alice 不能直接复制一份然后发给 Bob 吗?事实上,复制任意量子态是被禁止的,这可以用不可克隆定理来解释。证明如下,假设我们想要设计一个线路(幺正变换)U,它可以执行以下操作:
\begin{aligned}
U(\vert \psi \rangle \otimes \vert s \rangle) &= \vert \psi \rangle \otimes \vert \psi \rangle
\end{aligned}
\begin{aligned}
U(\vert \varphi \rangle \otimes \vert s \rangle) &= \vert \varphi \rangle \otimes \vert \varphi \rangle
\end{aligned}
其中\vert \psi\rangle和\vert \varphi\rangle是任意归一化的单量子比特态,\vert s \rangle是某个任意的归一化初始态。我们现在来证明这样的 U 是不存在的!
首先,让我们对等式左边取内积:
因为\langle s \vert s\rangle等于1,所以结果为\langle \psi \vert \varphi \rangle。接下来,我们比较等式右边的内积:(\langle \psi \vert \varphi
\rangle)^2。这两个内积必须相等,且只有当它们的值平方后仍等于自身时才成立。因此内积的取值只能是1或0。但如果内积为1,两个态是相同的;如果内积为0,两个态正交。所以,我们无法复制任意量子态!
解决方案:量子隐形传态
现在我们将一步一步地演示如何在不复制的情况下共享量子信息。
1. 态制备
隐形传态涉及三个量子比特。其中两个由Alice持有,第三个由Bob持有。我们用下标表示它们的状态:
–\vert\cdot\rangle_S,Alice 的第一个量子比特,她将其制备成某个任意态
–\vert\cdot\rangle_A,Alice 的辅助量子比特,她将其与 Bob 的量子比特纠缠用于通信
–\vert \cdot\rangle_B,Bob 的量子比特,将接收传送过来的态
它们的初始态为:
\vert 0\rangle_S \vert 0\rangle_A \vert 0\rangle_B.
Alice 首先要做的是将她的第一个量子比特制备成她想要发送给 Bob 的任意态
\vert \psi\rangle,这样它们的联合态就变成了:
\vert \psi\rangle_S \vert 0\rangle_A \vert 0\rangle_B.
2. 共享纠缠
隐形传态之所以有效,是因为利用了一个 Alice 和 Bob 之间共享的纠缠态资源。可以想象有一个过程生成了一对纠缠的量子比特,并将它们一一发送给双方。为了简单起见,我们将把产生纠缠的过程表示为线路的一部分。
将量子比特 A 和 B 纠缠后,联合态变为:
现在 AB 子系统处于一个所谓的 Bell 态。一共有四个极大纠缠的两量子比特 Bell 态,它们构成了 Bell 基:
\vert \psi_+\rangle = \frac{1}{\sqrt{2}} \left( \vert 00\rangle + \vert 11\rangle \right), \\
\vert \psi_-\rangle = \frac{1}{\sqrt{2}} \left( \vert 00\rangle – \vert 11\rangle \right), \\
\vert \phi_+\rangle = \frac{1}{\sqrt{2}} \left( \vert 01\rangle + \vert 10\rangle \right), \\
\vert \phi_-\rangle = \frac{1}{\sqrt{2}} \left( \vert 01\rangle – \vert 10\rangle \right).
在我们的实验中,因为 AB 起始态为 \vert 00\rangle,所以我们制备的是 \vert \psi_+\rangle Bell 态。为简洁起见,后面将省略量子态的下标。
3. 改变基底
传输协议的第三步是对前两个量子比特施加CNOT门和 Hadamard 门。这些操作在测量之前进行,被称为 “基底的改变”。但这指的是哪个基底呢?请注意,这两个量子门与我们创建 Bell 态时的操作恰好相反。如果反向运行它们,就能将基底转换回计算基底,从而模拟在 Bell 基底上的测量。
经过基底变换后,如果观测到前两个量子比特处于 \vert 00\rangle 态,这就对应于 Bell 基底中的 \vert \psi_+\rangle 态的结果;而 \vert 11\rangle 则对应于 \vert \phi_-\rangle,以此类推。让我们逐步执行这个基底的改变。
设初始态 \vert \psi\rangle 可以写成 \alpha\vert 0\rangle + \beta\vert 1\rangle 的形式,其中 \alpha 和 \beta 是复数系数。展开式中的各项,可得:
接下来,在 Alice 的两个量子比特之间施加一个 CNOT 门:
然后对她的第一个量子比特施加 Hadamard 门:
现在我们需要进行一些重新整理。将与前两个量子比特相关的项组合在一起:
4. 测量
协议的最后一步是 Alice 对她的量子比特进行测量,并根据测量结果告诉 Bob 进行某些操作。但为什么我们需要这样做呢?在前一步中,我们已经将基底旋转回了计算基底,难道还不够吗?不完全是,但也差不多了!
如果 Alice 在计算基底上测量她的两个量子比特,那么四种可能的结果出现的概率是相等的。如果她观测到前两个量子比特处于 \vert 00 \rangle 态,就立即知道 Bob 的量子比特正处于我们想要传输的目标态 \alpha \vert 0 \rangle + \beta \vert 1 \rangle!
如果她观测到的是 \vert 01\rangle 态,仍然能知道 Bob 的量子比特处于什么态,只不过与原态略有不同。具体来说:
\beta \vert 0 \rangle + \alpha \vert 1 \rangle = X \vert \psi \rangle
在得到这些结果后,Alice 可以告诉 Bob 对他的量子比特施加一个 X 门,就能恢复原始态。类似地,如果她得到的是 \vert 10\rangle 态,就会让他施加一个 Z 门。
事实上,在量子隐形传态的 “传统” 版本中[1],正是这么做的。Alice 会打电话给 Bob,告诉他她观测到了哪种态,然后他就能施加适当的校正。在这种情况下,测量发生在协议的中途,测量结果被用来控制后续量子门的应用。这就是所谓的中途测量(mid-circuit measurement)。
现在我们已经定义了量子隐形传态协议的所有基本组成部分。让我们把它们组合起来吧!
有一个巧妙的概念叫做测量延迟原理(principle of deferred measurement)[2],它基本上说明我们可以将所有的测量都推迟到线路的最后进行。这在许多情况下都很有用,比如在不支持中途测量的系统中工作时。
测量延迟原理带给我们的一个方案 —— 我们可以用一个 CNOT 门代替 Alice 打电话告诉 Bob 施加 X 门,CZ 门也是同理。这非常有用,因为它让我们能在任何测量发生之前就完成校正。让我们评估一下 CNOT 门和 CZ 门对 Bob 的量子比特的作用,确保 Alice 的态已经成功传输。施加 CNOT 门后得到:
再施加 CZ 门后得到:
当 Alice 最后测量她的两个量子比特时,无论得到哪种结果,Bob 的量子比特都将处于 \alpha\vert 0\rangle + \beta \vert 1\rangle 态。这意味着我们的协议已经将 Bob 的量子比特的状态变成了 Alice 想要发送的态!
我们将用它来验证 Alice 的态是否成功传输到了 Bob 的量子比特上。可以看到系统的最终态是:
现在,通过比较 Bob 最终的密度矩阵与 Alice 最初的密度矩阵,我们可以确认量子隐形传态协议成功实现了。
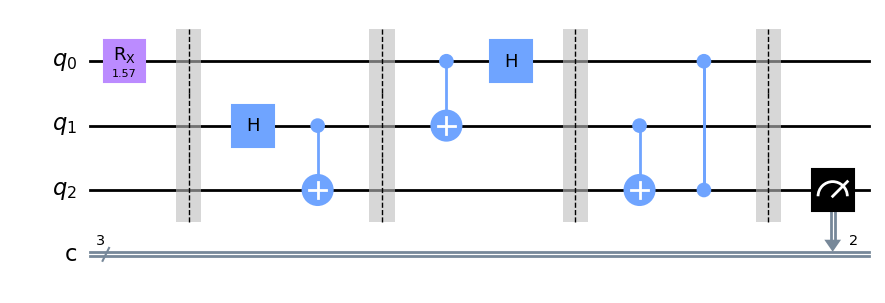
以下是用DeepQuantum设计的量子隐形传态实验线路图:
import deepquantum as dq
import numpy as np
def quantum_teleportation_circuit():
cir = dq.QubitCircuit(3)
# 1. 态制备
cir.rx(0,np.pi/2)
cir.barrier()
# 2. 共享纠缠
cir.h(1)
cir.cx(1, 2)
cir.barrier()
# 3. 改变基底
cir.cx(0, 1)
cir.h(0)
cir.barrier()
#4. 测量延迟
cir.cx(1, 2)
cir.cz(0, 2)
cir.measure(wires=2)
cir.barrier()
return cir
# 绘制量子线路图
teleportation_circuit = quantum_teleportation_circuit()
teleportation_circuit.draw()
结论
让我们回顾一下在本教程中学到的概念。首先,我们确定由于 “不可克隆定理”,量子态不能被任意复制。然后,我们了解了 “量子纠缠”。一旦 Alice 和 Bob 共享了一对纠缠的量子比特,Alice 就对它们执行了从 Bell 基底到计算基底的 “基底变换”。最后,在需要时利用 “测量延迟原理”,Alice 测量了她的两个量子比特,并指导 Bob 如何将他的量子比特旋转到目标态。
就这样,Alice 和 Bob 通过一个相当小的线路完成了量子隐形传态。由于需要 Alice 向 Bob 进行经典通信,量子态(也就是信息)仍然无法以超过光速的速度被传送。当然,这并不会削弱量子隐形传态的重要性,这个协议是量子信息处理中的一个关键工具。
参考文献
[1] Bennett C H, Brassard G, Crépeau C, et al. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels[J]. Physical review letters, 1993, 70(13): 1895.
[2] Nielsen M A, Chuang I L. Quantum computation and quantum information[M]. Cambridge university press, 2010.


