![]()
利用相位反冲构建量子锁
前言
在本文中,我们将探索量子相位反冲(phase kickback)的概念。这一概念在许多量子算法中都有应用,如Deutsch-Jozsa算法和量子相位估计算法。在本教程中,我们将利用相位反冲构建一个“量子锁”。准备好进入量子世界,学习如何创建一个牢不可破的锁了吗?让我们开始吧!
量子相位反冲简介
量子相位反冲是一种强大的量子现象,它利用量子纠缠的特性,将相位信息从目标寄存器传递到控制量子比特。这一现象在许多量子算法的设计中扮演着至关重要的角色。
在相位反冲线路中,我们先用Hadamard门将一个辅助量子比特制备成叠加态,使其作为控制比特。然后对目标寄存器施加一个受控幺正门。当目标寄存器处于幺正门的本征态时,相应本征值的相位会“反冲”到控制比特上。最后再对辅助量子比特施加一个Hadamard门,通过测量就能提取出相位信息。
构建量子锁
现在,让我们来创建宇宙中最强大的锁——“量子锁”!我们用幺正矩阵 U 来表示这个锁,除了一个特定的本征值为-1外,其余本征值均为1。我们将那个特殊的-1本征态称为“钥匙”态:
U|\text{key}\rangle = -|\text{key}\rangle
但是,当信息隐藏在相位中时,我们如何区分”钥匙”态和其他本征态呢?这就是相位反冲发挥作用的地方!当输入正确的本征态时,由 U 引入的-1相位会反冲到辅助比特上,使其状态从 |+\rangle 变为 |-\rangle 。此时,对控制比特的测量结果就能告诉我们输入态是否为正确的本征态。在这里, |1\rangle = H|-\rangle 表示解锁成功, |0\rangle = H|+\rangle 表示解锁失败。
为了简单起见,我们在计算基底下构建量子锁。在这种情况下,钥匙对应于一个二进制编码的整数 m,即我们的钥匙本征态:
\begin{aligned}
U|n\rangle =
\begin{cases}
-|n\rangle,&\text{if } n=m \\
|n\rangle,&\text{if } n\neq m
\end{cases}
\end{aligned}
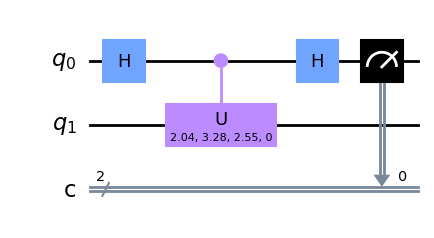
我们来构建这个锁:
import deepquantum as dq
cir = dq.QubitCircuit(2)
# 加 Hadamard 门
cir.h(0)
# 受控U矩阵
cir.cu(0,1)
# 加 Hadamard 门
cir.h(0)
# 测量
cir.measure(wires=0)
# 绘制图片
cir.draw()
c:\Users\HP\.conda\envs\dq\lib\site-packages\qiskit\visualization\circuit\matplotlib.py:266: FutureWarning: The default matplotlib drawer scheme will be changed to "iqp" in a following release. To silence this warning, specify the current default explicitly as style="clifford", or the new default as style="iqp".
self._style, def_font_ratio = load_style(self._style)
接下来,我们需要根据想要尝试的钥匙来制备相应的本征态。请记住,只有具有-1本征值的”钥匙”态才能打开锁。我们来构建钥匙态:
假设 U 为泡利矩阵 Z, |\text{key}\rangle= \begin{bmatrix} 0\\1 \end{bmatrix},|\text{incorrect key}\rangle= \begin{bmatrix} 1\\0 \end{bmatrix}
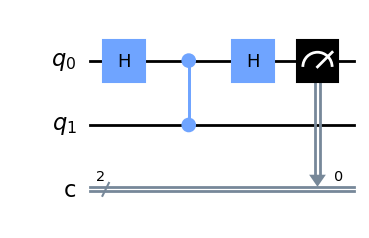
现在,我们将这些组件组合起来,构建完整的量子锁机制:
def quantum_locking_mechanism():
cir = dq.QubitCircuit(2)
# 加 Hadamard 门
cir.h(0)
# 加 CZ 门
cir.cz(0,1)
# 加 Hadamard 门
cir.h(0)
# 测量
cir.measure(wires=0)
return cir
# 绘制图片
cir=quantum_locking_mechanism()
cir.draw()
打开量子锁
要打开量子锁,我们需要正确的输入态,即”量子钥匙”。让我们看看当输入正确钥匙时,量子系统如何演化。
首先对控制比特施加Hadamard门:
\frac{|0\rangle|\text{key}\rangle + |1\rangle|\text{key}\rangle}{\sqrt{2}}
再施加受控幺正门,得到:
\frac{|0\rangle|\text{key}\rangle – |1\rangle|\text{key}\rangle}{\sqrt{2}} = |-\rangle|\text{key}\rangle
最后,再次对控制比特施加Hadamard门,得到:
|1\rangle|\text{key}\rangle
就这样,我们解开了量子锁隐藏的秘密。接下来,让我们在代码中实践一下!
def quantum_locking_mechanism():
cir = dq.QubitCircuit(2)
# 加 Hadamard 门
cir.h(0)
# 受控U矩阵
cir.cz(0,1)
# 加 Hadamard 门
cir.h(0)
# 测量
cir.measure()
return cir
cir=quantum_locking_mechanism()
cir()
tensor([[1.0000+0.j],
[0.0000+0.j],
[0.0000+0.j],
[0.0000+0.j]])
使用错误钥匙会怎样?
现在,我们尝试使用错误的钥匙,看看能否打开量子锁。我们能突破它的量子防御吗?让我们看看输入错误钥匙时,量子系统会如何演化。
首先对控制比特施加Hadamard门:
在这种情况下,受控幺正门相当于单位门,因此我们得到:
最后,再次对控制比特施加Hadamard门,得到:
|0\rangle|\text{incorrect key}\rangle
如你所见,我们无法欺骗这个强大的锁。
def quantum_locking_mechanism():
cir = dq.QubitCircuit(2)
cir.x(1)
# 加 Hadamard 门
cir.h(0)
# 受控U矩阵
cir.cz(0,1)
# 加 Hadamard 门
cir.h(0)
# 测量
cir.measure()
return cir
cir=quantum_locking_mechanism()
cir()
tensor([[0.0000+0.j],
[0.0000+0.j],
[0.0000+0.j],
[1.0000+0.j]])
结论
你已经成功探索了非凡的相位反冲现象,并创造了一个牢不可破的“量子锁”。


