![]()
混合量子经典循环神经网络
搭建量子RNN网络
本节内容将详细介绍混合量子经典循环神经网络(Quantum Recurrent Neural Network,简称 QRNN)的构建过程,并展示其在量子模拟器上的模型架构与实验效果[1] [2]。混合量子经典循环神经网络是传统循环神经网络(Recurrent Neural Network,简称 RNN)的量子化版本,其主要特点在于将 RNN 单元中的全连接层替换为变分量子线路(Variational Quantum Circuit,简称 VQC),同时保留了单元中原有的计算逻辑。通过本节的学习,您将深入理解混合量子经典循环神经网络的基础理论、实现方法,以及在解决实际问题时的应用案例。在探究量子RNN模型的搭建之前,首先需了解其核心组成部分——变分量子线路(Variational Quantum Circuit, VQC)。变分量子线路(VQC),也被称为参数化量子线路(Parameterized Quantum Circuit, PQC),通常包含三个关键部分:状态制备、变分量子线路和测量。下图中 U(x) 表示状态制备线路,它的作用是将经典数据 x 编码为量子态。 V(\theta) 表示具有可调节参数 \theta 的变分线路,可以通过梯度下降的方法进行优化。最后通过测量量子态,得到经典的输出值[1] [2]。
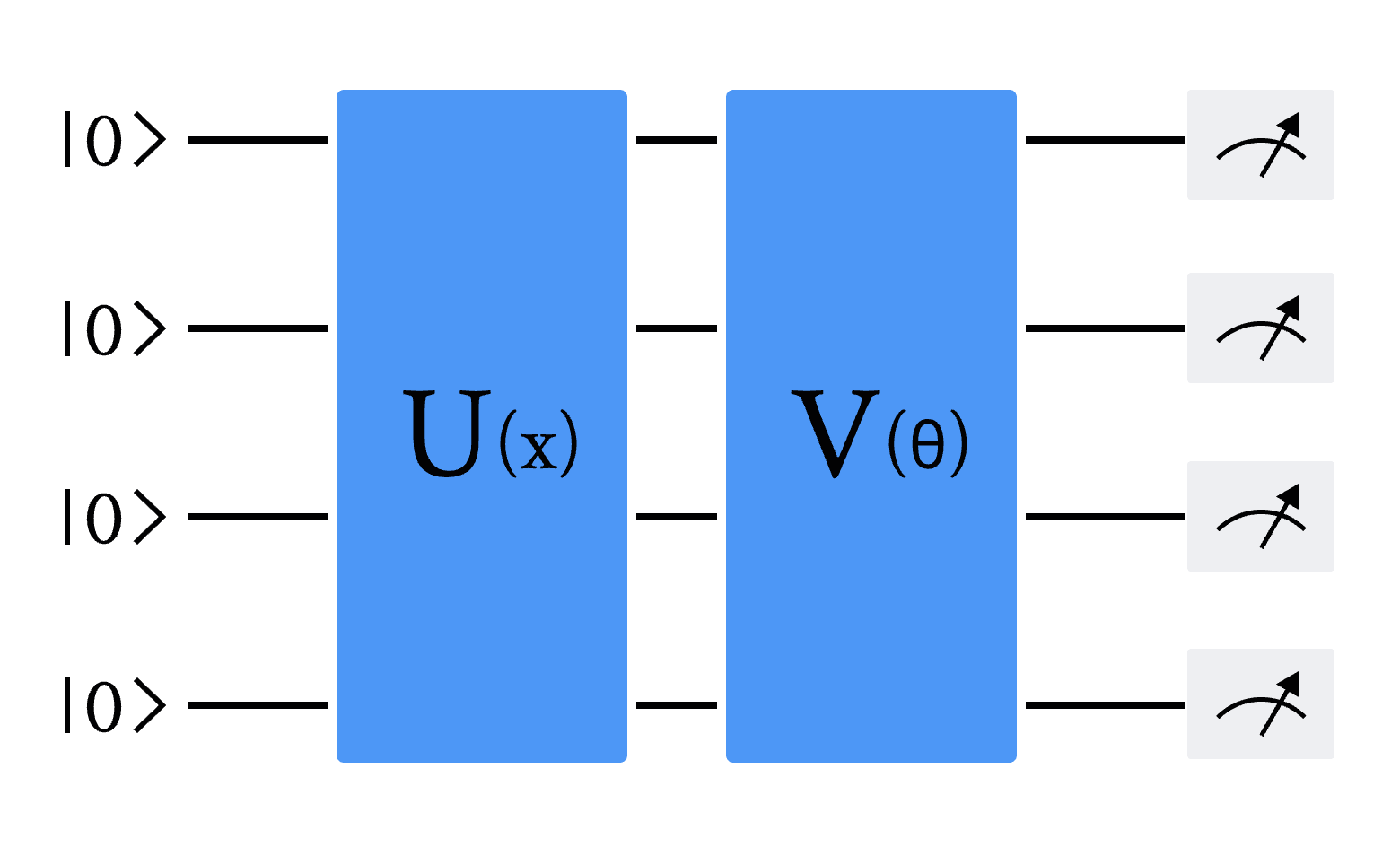
图 1 变分量子线路(VQC)的通用架构。U(x) 是将经典输入数据 x 编码为量子态的量子线路,V(θ) 是具有可调节或可学习参数 θ 的变分线路。线路最后是对部分或全部量子比特的测量
在这里,我们通过 DeepQuantum 去实现一个用于 QRNN 的 VQC 模块(图1),包括以下三个部分: 编码线路、变分线路和量子测量。
1.编码线路
编码线路将经典数据值映射为量子振幅。量子线路先进行基态初始化,然后利用 Hadamard 门来制备无偏初始态。我们使用双角编码(two-angle encoding),用两个角度编码一个值,将每个数据值分别用两个量子门( Ry 和 Rz )进行编码。两个量子门的旋转角度分别为:f(x _i) = \arctan(x _i) 和 g(x _i) = \arctan(x _i^2) ,其中 x _i 是数据向量 x 的一个分量。编码数据的量子态为[1]:
其中 N 是向量 x 的维数,\pi /4 的角偏移是因为初始的 Hadamard 门旋转。
2.变分线路
变分量子线路由几个 CNOT 门和单量子比特旋转门组成。CNOT门以循环的方式作用于每一对位置距离1和2的量子比特,用于产生纠缠量子比特。可学习参数 \alpha , \beta 和 \gamma 控制单量子比特旋转门,它们可以基于梯度下降算法进行迭代优化更新。该变分量子线路模块可以重复多次,以增加变分参数的数量。
3.量子测量
VQC块的末端是一个量子测量层,我们通过测量来计算每个量子态的期望值。在量子模拟软件中,我们可以在经典计算机上进行数值计算,而在真实的量子计算机中,这些数值是通过重复测量进行统计估计得到的。
# 首先我们导入所有需要的包:
import torch
import torch.nn as nn
import deepquantum as dq
import matplotlib.pyplot as plt
import numpy as np
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
import pandas as pd
# 我们设计的VQC线路如下 这里我们以4个bit作为例子
cir = dq.QubitCircuit(4)
cir.hlayer()
cir.rylayer(encode=True)
cir.rzlayer(encode=True)
cir.barrier()
cir.cnot_ring()
cir.barrier()
cir.cnot_ring(step=2)
cir.barrier()
cir.u3layer()
cir.barrier()
cir.measure()
cir.draw() # 画出量子线路图
c:\Users\HP\.conda\envs\dq\lib\site-packages\qiskit\visualization\circuit\matplotlib.py:266: FutureWarning: The default matplotlib drawer scheme will be changed to "iqp" in a following release. To silence this warning, specify the current default explicitly as style="clifford", or the new default as style="iqp".
self._style, def_font_ratio = load_style(self._style)
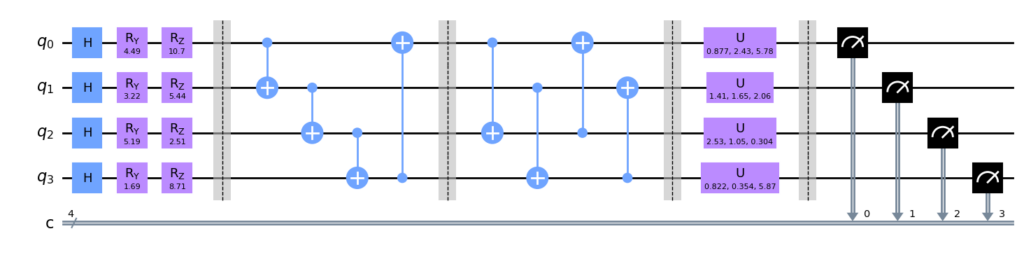
VQC 模块由三个主要部分构成:编码线路、变分线路以及量子测量。编码线路包含 H 门、Ry 门和 Rz 门,负责将信息编码至量子态。变分线路位于第1条和第4条虚线之间,其结构可以根据需要调整。量子比特的数量和量子测量的次数均可按实验需求进行灵活配置。此外,变分线路的层数和参数数量可以增加,以扩展模型规模,这主要取决于所使用的量子计算机或量子模拟软件的处理能力。在本节的示例中,所用的量子比特数量为4个。
量子RNN模型
在讲解量子 RNN 模型前,我们先简单回顾一下经典 RNN 模型的原理和结构(图2)。我们使用数学公式描述经典 RNN 模型的计算单元:
其中 W_{ih} 是作用在 x_t 上的隐藏层权重参数, b_{ih} 是对应的隐藏层偏差参数, W_{hh} 是作用在 h_{t-1} 上的隐藏层权重参数, b_{hh} 是对应的隐藏层偏差参数,这里使用 tanh 函数作为激活函数。
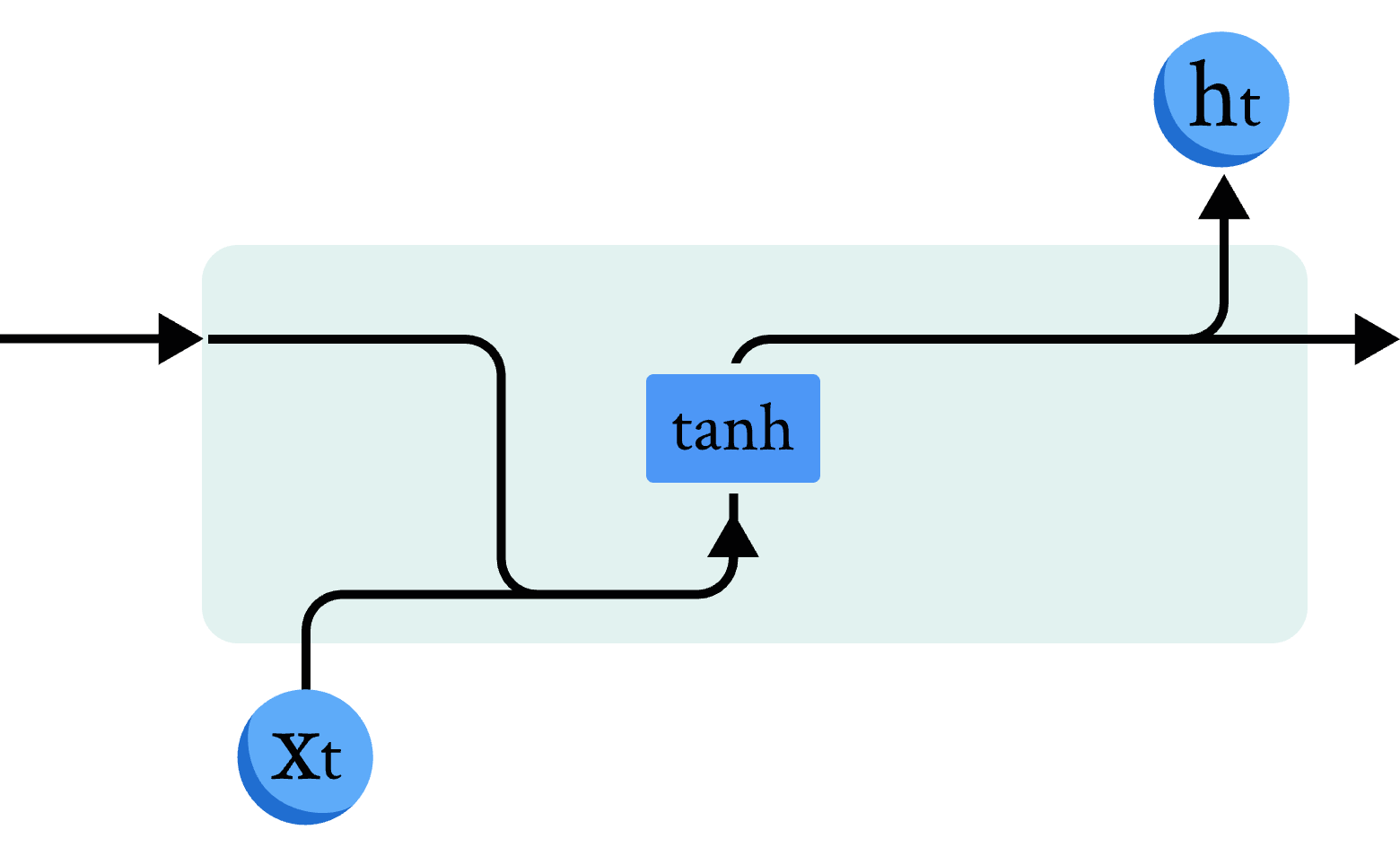
图 2 经典RNN模型示意图
量子 RNN 模型是经典 RNN 模型的量子版本。主要区别在于经典神经网络被 VQC 取代,我们使用数学公式描述 QRNN 模型的计算单元 [1]:
h_t = \tanh(VQC(v_t))
y_t = NN(h_t)
其中输入 v_t 是前一个时间步长的隐藏状态 h_{t−1} 与当前输入向量 x_t 的级联, NN 是经典神经网络层。
首先我们先用DeepQuantum实现一个VQC模块:
## 定义VQC模块
class QuLinear(nn.Module):
def __init__(self, input_size, hidden_size):
super(QuLinear, self).__init__()
n_qubits = input_size #定义比特个数
self.cir = dq.QubitCircuit(n_qubits, reupload=True)
self.cir.hlayer()
self.cir.rylayer(encode=True)
self.cir.rzlayer(encode=True)
self.cir.barrier()
self.cir.cnot_ring()
self.cir.barrier()
self.cir.cnot_ring(step=2)
self.cir.barrier()
self.cir.u3layer()
self.cir.barrier() #两层变分线路模块[1]
self.cir.cnot_ring()
self.cir.barrier()
self.cir.cnot_ring(step=2)
self.cir.barrier()
self.cir.u3layer()
for i in range(hidden_size): # 以for循环
self.cir.observable(wires=i, basis='z')
def forward(self, x):
ry_parameter = torch.arctan(x) #将经典数据转化为对应ry的角度
rz_parameter = torch.arctan(x*x) #将经典数据转化为对应rz的角度
r_parameter=torch.cat([ry_parameter,rz_parameter],dim=1)
self.cir(r_parameter)
return self.cir.expectation()
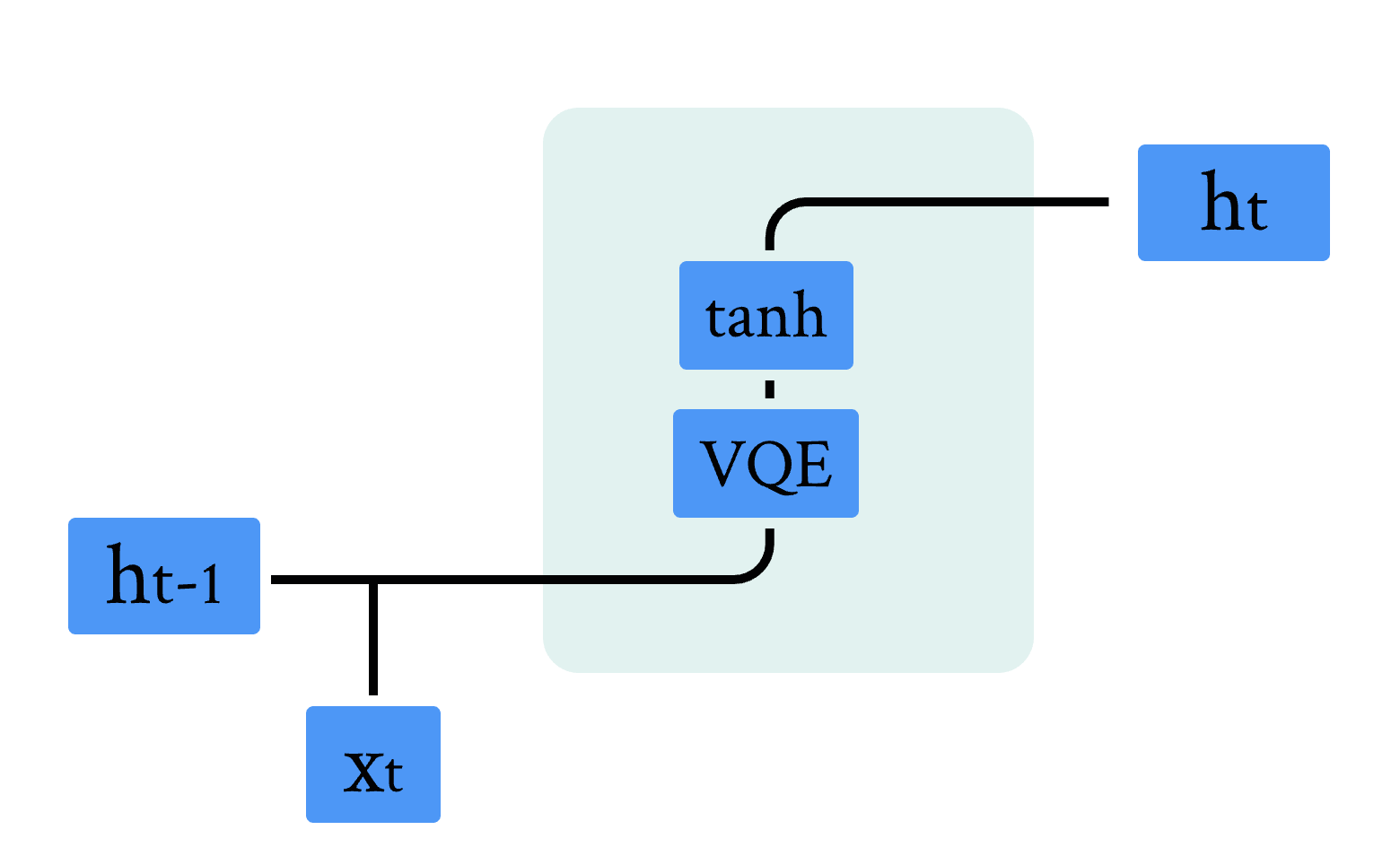
图 3 量子RNN模型示意图
图 3 展示了混合量子经典 RNN 的单元结构,结合前面章节的内容,不难发现,相比于经典结构,其中的线性全连接层被 VQC 线路替换,我们可以利用上面我们实现的 QuLinear,结合经典 RNN 的计算逻辑,实现量子混合经典循环神经网络。代码如下:
class QRNNCell(nn.Module):
def __init__(self, input_size, hidden_size):
super(QRNNCell, self).__init__()
self.input_size = input_size
self.hidden_size = hidden_size
self.linear = QuLinear(input_size+hidden_size, hidden_size)
self.tanh = nn.Tanh()
def forward(self, x, h):
v = torch.cat((x, h), dim=-1)
h = self.tanh(self.linear(v))
return h
class QRNN_hybrid(nn.Module):
def __init__(self, input_size, hidden_size, target_size, device):
super(QRNN_hybrid, self).__init__()
self.input_size = input_size
self.hidden_size = hidden_size
self.h0_linear = nn.Linear(hidden_size, hidden_size)
self.gru = QRNNCell(input_size, hidden_size)
self.tanh = nn.Tanh()
self.device = device
self.predictor = nn.Linear(hidden_size, target_size)
def forward(self, x, hidden_state=None):
# 初始化隐藏状态
if hidden_state is None:
batch_size, sequence_length, _ = x.size()
h0 = self.tanh(self.h0_linear(torch.zeros(batch_size, self.hidden_size).to(self.device))).to(self.device)
# 存储所有时间步的隐藏状态
hidden_states = []
# 遍历所有时间步
for t in range(sequence_length):
xt = x[:, t, :]
ht = self.gru(xt, h0)
hidden_states.append(ht.unsqueeze(1))
h0 = ht
output = self.predictor(torch.cat(hidden_states, dim=1))
return output, hidden_states[-1]
else:
ht = self.gru(x[:, -1].unsqueeze(1), hidden_state)
output = self.predictor(ht)
return output, ht
# 测试模型代码能否成功运行
# 定义输入、隐藏状态和输出的维度
input_size = 2 #输入
hidden_size = 3
output_size = 1 #输出一个数值
# 创建模型实例
device = torch.device("cpu")
model = QRNN_hybrid(input_size, hidden_size, output_size, device)
# 随机生成输入数据
batch_size = 3
sequence_length = 4
input_data = torch.randn(batch_size, sequence_length, input_size)
# 前向传播
output, _ = model(input_data)
# 输出结果
print("输出的形状:", output.shape)
输出的形状: torch.Size([3, 4, 1])
量子RNN模型训练
本节将介绍量子 RNN 模型训练过程,包括训练的数据介绍,训练过程的代码实现。
数据任务
在这里,我们使用余弦函数作为模型训练的数据集,首先定义数据集构建函数,代码如下:
#构建时间序列数据集
class TimeSeriesDataset(Dataset):
def __init__(self, data, sequence_length):
self.data = data
self.sequence_length = sequence_length #定义数据长度
self.xdata = []
self.ydata = []
for i in range(len(data)):
if i + self.sequence_length + 1 > len(data):
break
self.xdata.append(self.data[i:i+self.sequence_length]) #xdata为输入数据
self.ydata.append(self.data[i+1:i+self.sequence_length+1]) #ydata为需要预测的后一位输出数据
def __len__(self):
return len(self.xdata)
def __getitem__(self, index):
x = self.xdata[index]
y = self.ydata[index] # 目标序列错开一位
return x, y
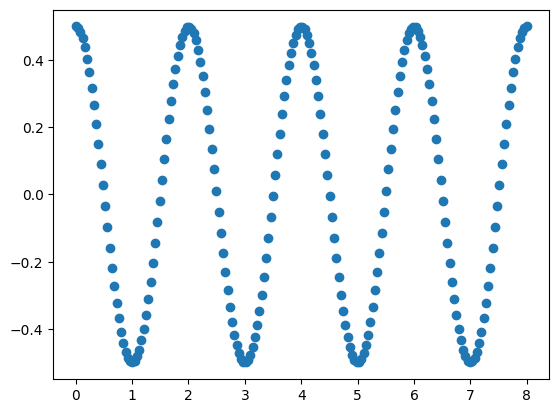
我们给出范围在 [0, 8\pi] 的余弦函数,振幅为0.5,将其分为200个数据点,取前100个数据点作为模型的训练数据,代码如下:
start = 0
end = 8
data_points = 200
amplitude = 0.5
num_train_points = 100
time_steps = np.linspace(start, end, data_points) # 在区间[0, 8*pi]之间线性均匀的选择200个数据点
data = np.cos(np.pi*time_steps)*amplitude # 生成区间[0, 8*pi]上的余弦信号时间序列数据
train_data = data[:num_train_points] # 选择前100个数据点作为训练集
test_data = data[num_train_points:]
# 创建数据集对象
# 由于第一个数据点不需要预测 而序列的最后一个数据点不能出现在训练的输入特征中 这里特征序列和标签序列的长度都需要设为总长度-1
sequence_length = num_train_points - 1
dataset = TimeSeriesDataset(torch.tensor(train_data), sequence_length)
# 创建数据加载器
# 这里我们不做数据的窗口切分,因此每个batch中只有一条完整数据,并且只有一个batch
batch_size = 1
dataloader = DataLoader(dataset, batch_size=batch_size)
#画出我们的数据集
plt.plot(time_steps, data,'o')
plt.show()
全参数训练
在接下来的实验中,我们将利用上一小节中准备的数据集,以及基于上一节构建的 QRNN 模型来进行模型训练。实验中采用均方差损失函数(Mean Squared Error Loss,简称 MSELoss)作为训练过程中的损失函数。选用的优化器为 RMSprop[1],这是一种基于梯度下降法的变体,它具备自适应学习率调整的特性。优化器的超参数配置如下:平滑常数alpha设为0.99,eps设为1e−8,动量(momentum)设为0.5。下面是定义模型训练函数的代码:
def trainer(model, epoch, learning_rate, device):
criterion = nn.MSELoss()
optimizer = torch.optim.RMSprop(model.parameters(),learning_rate,alpha=0.99,eps=1e-08,weight_decay=0,momentum=0.5,centered=False)
model = model.to(device)
flag = False
train_loss_list=[]
for e in range(epoch):
if flag:
break
for x, y in dataloader:
x = x.unsqueeze(-1).float()
y = y.unsqueeze(-1).float()
x = x.to(device)
y = y.to(device)
y_pred, _ = model(x)
loss = criterion(y_pred, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
train_loss_list.append(loss.detach().numpy())
print("Iteration: {} loss {}".format(e, loss.item()))
metrics = {'epoch': list(range(1, len(train_loss_list)+1)),
'train_loss': train_loss_list}
return model, metrics
我们设置优化器的学习率 lr 为0.01,迭代次数为100次,模型中 VQC 的输入量子比特个数为1,隐藏层量子比特个数为3,输出量子比特个数为1。分别训练 QRNN,QLSTM 和 QGRU 模型,代码如下:
# 训练混合量子经典RNN
lr = 0.01 #定义学习率为0.01
epoch = 100 #定义迭代次数为100次
device = torch.device("cpu")
model_QRNN = QRNN_hybrid(1, 3, 1, device)
optim_model, metrics=trainer(model_QRNN, epoch, lr, device)
Iteration: 0 loss 0.2551746368408203
Iteration: 50 loss 0.002133062342181802
Iteration: 99 loss 0.0015379682881757617
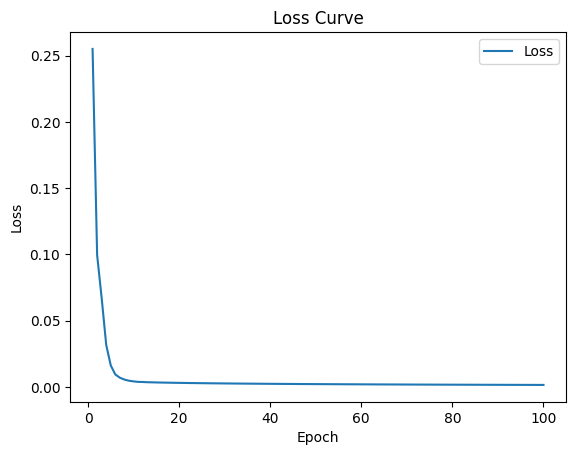
# 绘制QRNN模型的loss曲线
epoch = metrics['epoch']
loss = metrics['train_loss']
# 创建图和Axes对象
# 绘制训练损失曲线
plt.plot(epoch, loss, label='Loss')
plt.title('Loss Curve')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.legend()
参考文献
[1] Chen, S. Y. C., Fry, D., Deshmukh, A., Rastunkov, V., & Stefanski, C. (2022). Reservoir computing via quantum recurrent neural networks. arXiv preprint arXiv:2211.02612.
[2] Chen, S. Y. C., Yoo, S., & Fang, Y. L. L. (2022, May). Quantum long short-term memory. In ICASSP 2022-2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (pp. 8622-8626). IEEE.


