![]()
量子密钥分发
1. 引言
当Alice和Bob想要通过不安全的信道(如互联网)传递一个秘密消息(如Bob的网上银行信息)时,对消息进行加密是至关重要的。密码学要求Alice和Bob拥有一个只有他们知道的秘密密钥,这个密钥允许他们使用对称密钥加密进行通信。
如果Alice和Bob想使用Eve的经典通信信道来共享他们的密钥,就无法判断Eve是否为自己制作了这个密钥的副本——他们必须完全信任Eve没有窃听。然而,如果Eve提供了一个量子通信信道,Alice和Bob就不再需要信任Eve了——如果Eve试图在Bob的消息到达Alice之前读取它,他们就会知道。
对于一些读者而言,了解如何在物理层面上构建量子信道可能颇具帮助。举一个经典信道的例子,比如电话线;我们通过电话线传送代表信息(或比特)的电信号。而一个典型的量子通信信道的例子是光纤,通过该光纤我们可以发送单个光子。光子具有一种称为偏振的属性,该偏振能呈现出两种不同的状态。我们可以利用这一特性来表达一个量子比特。
2. 协议概述
该协议利用了测量量子比特可以改变其状态这一事实。如果Alice向Bob发送一个量子比特,而窃听者(Eve)试图在Bob之前测量它,那么Eve的测量有可能改变量子比特的状态,Bob就不会接收到Alice发送的量子比特状态。
如果Alice将一个量子比特制备成 |+\rangle 态(0在 X 基向量中),而Bob在 X 基向量中测量它,那么Bob一定会测量到0:
但是,如果Eve试图在量子比特到达Bob之前在 Z 基向量中测量它,她将把量子比特的状态从 |+\rangle 改变为 |0\rangle 或 |1\rangle,Bob就不再一定测量到0,而是有50%的几率测量到1,如果他真的测量到了1,他和Alice就会知道他们的信道出了问题。
量子密钥分发协议需要重复这个过程足够多次,使窃听者几乎没有机会逃脱拦截的可能。大致过程如下:
– 第1步
Alice选择一串随机比特,例如:
1000101011010100
以及每个比特随机选择的基向量:
ZZXZXXXZXZXXXXXX
Alice将这两条信息保密。
– 第2步
然后Alice使用她选择的基向量将每个比特编码到一串量子比特上;这意味着每个量子比特都处于随机选择的状态 |0\rangle、|1\rangle、|+\rangle 或 |-\rangle 之一。在本例中,量子比特串如下所示:
这就是她发送给Bob的消息。
– 第3步
然后Bob随机测量每个量子比特,例如,他可能使用以下基向量:
XZZZXZXZXZXZZZXZ
Bob将测量结果保密。
– 第4步
然后Bob和Alice公开分享他们对每个量子比特使用的基向量。如果Bob用与Alice制备量子比特时相同的基向量测量了一个量子比特,他们就用这个结果来形成部分共享的秘密密钥,否则就丢弃该比特的信息。
– 第5步
最后,Bob和Alice共享他们密钥的随机样本,如果样本匹配,他们就可以确定(在一个小的误差范围内)他们的传输是成功的。
3. DeepQuantum示例:无拦截情况
让我们首先看看在没有人窃听的情况下协议是如何工作的,然后我们可以看到Alice和Bob如何能够检测到窃听者。
3.1 第1步:
为了生成伪随机密钥,我们将使用numpy的 randint 函数。为了确保你能重现本页面上的结果,我们将种子设置为0。
我们将Alice初始消息的长度称为 n。在这个例子中,Alice将发送一个100个量子比特长的消息。
Alice生成她的随机比特集:
from numpy.random import randint
import numpy as np
import deepquantum as dq
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
print(alice_bits)
[0 1 1 0 1 1 1 1 1 1 1 0 0 1 0 0 0 0 0 1 0 1 1 0 0 1 1 1 1 0 1 0 1 0 1 1 0
1 1 0 0 1 0 1 1 1 1 1 0 1 0 1 1 1 1 0 1 0 0 1 1 0 1 0 1 0 0 0 0 0 1 1 0 0
0 1 1 0 1 0 0 1 0 1 1 1 1 1 1 0 1 1 0 0 1 0 0 1 1 0]
此时,比特集 alice_bits 只有Alice知道。我们将跟踪只有Alice知道的信息、只有Bob知道的信息以及通过Eve的信道发送的信息,如下表所示:
| Alice知道的信息 | 通过Eve的信道 | Bob知道的信息 |
|---|---|---|
| alice_bits |
3.2 第2步:
Alice随机选择在 X 或 Z 基向量中对每个比特进行编码,并将每个量子比特的选择存储在 alice_bases 中。在本例中,0 表示”在 Z 基向量中制备”,1 表示”在 X 基向量中制备”:
np.random.seed(seed=0)
n = 100
## Step 1
#Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
print(alice_bases)
[1 0 0 1 0 0 0 1 1 0 1 0 0 0 0 0 1 0 1 0 1 1 1 1 1 0 1 1 1 1 0 1 1 0 0 1 0
0 0 0 1 1 0 0 1 0 1 1 1 1 0 0 0 1 0 1 1 1 0 1 0 0 1 0 1 1 0 0 1 0 1 0 1 0
1 0 1 0 0 0 1 0 1 0 1 0 0 0 0 0 1 0 0 1 0 0 0 1 0 0]
Alice也对这一知识保密:
| Alice知道的信息 | 通过Eve的信道 | Bob知道的信息 |
|---|---|---|
| alice_bits | ||
| alice_bases |
下面的 encode_message 函数创建了一个 QuantumCircuit 的列表,每个线路代表Alice消息中的一个量子比特:
def encode_message(bits, bases):
message = []
for i in range(n):
cir = dq.QubitCircuit(1)
if bases[i] == 0: # Prepare qubit in Z-basis
if bits[i] == 0:
pass
else:
cir.x(0)
else: # Prepare qubit in X-basis
if bits[i] == 0:
cir.h(0)
else:
cir.x(0)
cir.h(0)
cir.barrier()
message.append(cir)
return message
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
我们可以看到 alices_bits 中的第一个比特是 0,她对它进行编码的基向量是 X 基向量(用 1 表示):
print('bit = %i' % alice_bits[0])
print('basis = %i' % alice_bases[0])
bit = 0
basis = 1
如果我们查看 message 中的第一个线路(代表Alice消息中的第一个量子比特),我们可以验证Alice已经制备了一个状态为 |+\rangle 的量子比特:
message[0].draw()
c:\Users\HP\.conda\envs\dq\lib\site-packages\qiskit\visualization\circuit\matplotlib.py:266: FutureWarning: The default matplotlib drawer scheme will be changed to "iqp" in a following release. To silence this warning, specify the current default explicitly as style="clifford", or the new default as style="iqp".
self._style, def_font_ratio = load_style(self._style)
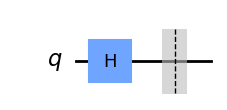
另一个例子是,我们可以看到 alice_bits 中的第四个比特是 1,它在 Z 基向量中编码,Alice将相应的量子比特制备成 |1\rangle 态:
print('bit = %i' % alice_bits[4])
print('basis = %i' % alice_bases[4])
message[4].draw()
bit = 1
basis = 0
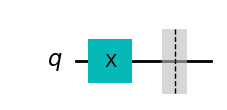
然后这个量子比特消息通过Eve的量子信道发送给Bob:
| Alice知道的信息 | 通过Eve的信道 | Bob知道的信息 |
|---|---|---|
| alice_bits | ||
| alice_bases | ||
| message | message | message |
3.3 第3步:
Bob随机选择X基或Z基测量每个量子比特,并存储这些信息:
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Step 3
# Decide which basis to measure in:
bob_bases = randint(2, size=n)
print(bob_bases)
[1 0 1 0 0 1 1 0 0 0 1 1 0 0 0 0 0 1 0 1 0 0 0 1 1 1 0 0 1 1 1 1 0 0 0 1 1
0 1 0 0 1 0 1 1 1 1 0 0 0 1 1 1 0 1 1 1 1 0 0 1 1 0 0 0 1 1 0 1 1 1 1 1 0
0 0 1 0 1 0 1 1 0 0 0 1 0 0 1 1 1 1 0 1 0 0 0 0 1 1]
下面,measure_message函数对每个量子比特应用相应的测量,并模拟测量结果。我们将测量结果存储在bob_results中。
def measure_message(message, bases):
measurements = []
for q in range(n):
if bases[q] == 1: # measuring in X-basis
message[q].h(0)
message[q]()
qobj = message[q].measure(shots=1)
measured_bit = int(list(qobj.keys())[0])
measurements.append(measured_bit)
return measurements
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Step 3
# Decide which basis to measure in:
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
我们可以看到,代表第0个量子比特的线路message[0]被Bob添加了X测量:
message[0].draw()
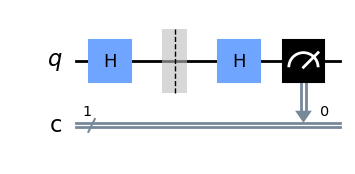
由于Bob恰好选择了与Alice编码该量子比特相同的基,Bob必然会得到结果0。对于第6个量子比特(如下所示),Bob随机选择的测量与Alice的不同,Bob的结果只有50%的概率与Alice的匹配。
message[6].draw()
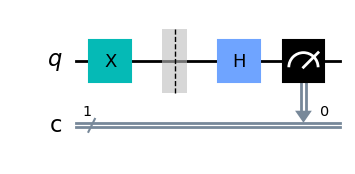
print(bob_results)
[0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0]
Bob对他的测量结果保密。
| Alice的知道的信息 | 经过Eve的信道 | Bob的知道的信息 |
|---|---|---|
| alice_bits | ||
| alice_bases | ||
| message | message | message |
| bob_bases | ||
| bob_results |
3.4 第4步:
此后,Alice 通过 Eve 的频道公开了每个量子比特是用哪种基态编码的:
| Alice的知道的信息 | 经过Eve的信道 | Bob的知道的信息 |
|---|---|---|
| alice_bits | ||
| alice_bases | ||
| message | message | message |
| bob_bases | ||
| bob_results | ||
| alice_bases | alice_bases |
然后 Bob 公开他测量每个量子比特所用的基态:
| Alice的知道的信息 | 经过Eve的信道 | Bob的知道的信息 |
|---|---|---|
| alice_bits | ||
| alice_bases | ||
| message | message | message |
| bob_bases | ||
| bob_results | ||
| alice_bases | alice_bases | |
| bob_bases | bob_bases |
如果 Bob 恰好使用 Alice 准备的相同基态测量了某个比特,这意味着 bob_results 中的相应条目将与 alice_bits 中的相应条目匹配,他们可以将该比特作为他们密钥的一部分。如果他们使用不同的基态进行测量,Bob 的结果就是随机的,他们都需要丢弃该条目。以下是一个名为 remove_garbage 的函数,它为我们完成了这项工作:
def remove_garbage(a_bases, b_bases, bits):
good_bits = []
for q in range(n):
if a_bases[q] == b_bases[q]:
# 如果双方使用了相同的基态,将其添加到“好”比特的列表中
good_bits.append(bits[q])
return good_bits
Alice和Bob都丢弃无用的比特,使用剩下的比特形成他们的秘钥:
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Step 3
# Decide which basis to measure in:
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
## Step 4
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
print(alice_key)
[0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0]
Alice和Bob都丢弃无用的比特,使用剩下的比特形成他们的秘密密钥:
| Alice的知道的信息 | 经过Eve的信道 | Bob的知道的信息 |
|---|---|---|
| alice_bits | ||
| alice_bases | ||
| message | message | message |
| bob_bases | ||
| bob_results | ||
| alice_bases | alice_bases | |
| bob_bases | bob_bases | |
| alice_key |
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Step 3
# Decide which basis to measure in:
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
## Step 4
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
print(bob_key)
[0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0]
| Alice的知道的信息 | 经过Eve的信道 | Bob的知道的信息 |
|---|---|---|
| alice_bits | ||
| alice_bases | ||
| message | message | message |
| bob_bases | ||
| bob_results | ||
| alice_bases | alice_bases | |
| bob_bases | bob_bases | |
| alice_key | bob_key |
3.5 第5步:
最后,Bob和Alice比较他们密钥中随机选择的一些比特,以确保协议正确工作:
def sample_bits(bits, selection):
sample = []
for i in selection:
# use np.mod to make sure the
# bit we sample is always in
# the list range
i = np.mod(i, len(bits))
# pop(i) removes the element of the
# list at index 'i'
sample.append(bits.pop(i))
return sample
Alice和Bob都公开这些比特,并从密钥中删除,因为它们不再是秘密:
np.random.seed(seed=0)
n = 100
## Step 1
# Alice generates bits
alice_bits = randint(2, size=n)
## Step 2
# Create an array to tell us which qubits
# are encoded in which bases
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Step 3
# Decide which basis to measure in:
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
## Step 4
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
## Step 5
sample_size = 15
bit_selection = randint(n, size=sample_size)
bob_sample = sample_bits(bob_key, bit_selection)
print(" bob_sample = " + str(bob_sample))
alice_sample = sample_bits(alice_key, bit_selection)
print("alice_sample = "+ str(alice_sample))
bob_sample = [0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0]
alice_sample = [0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0]
| Alice的知道的信息 | 经过Eve的信道 | Bob的知道的信息 |
|---|---|---|
| alice_bits | ||
| alice_bases | ||
| message | message | message |
| bob_bases | ||
| bob_results | ||
| alice_bases | alice_bases | |
| bob_bases | bob_bases | |
| alice_key | bob_key | |
| bob_sample | bob_sample | bob_sample |
| alice_sample | alice_sample | alice_sample |
如果协议正确工作且没有干扰,他们的样本应该匹配:
bob_sample == alice_sample
True
如果他们的样本匹配,这意味着(以很高的概率)alice_key == bob_key。现在他们共享了一个秘密密钥,可以用来加密他们的消息!
| Alice的知道的信息 | 经过Eve的信道 | Bob的知道的信息 |
|---|---|---|
| alice_bits | ||
| alice_bases | ||
| message | message | message |
| bob_bases | ||
| bob_results | ||
| alice_bases | alice_bases | |
| bob_bases | bob_bases | |
| alice_key | bob_key | |
| bob_sample | bob_sample | bob_sample |
| alice_sample | alice_sample | alice_sample |
| shared_key | shared_key |
4. DeepQuantum示例:有窃听
现在让我们看看,如果Eve试图窃听他们的量子消息,Alice和Bob如何发现。我们重复之前没有干扰时的相同步骤,但在Bob收到量子比特之前,Eve会试图从中提取一些信息。让我们设置一个不同的随机种子,以获得一组特定的可重复的随机结果。
4.1 第1步:
Alice生成一组随机比特:
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
print(alice_bits)
[0 0 1 1 0 0 0 1 1 1 0 1 1 1 0 1 1 0 0 0 0 1 1 0 0 0 1 0 0 0 0 1 0 1 1 0 1
0 0 1 1 0 0 1 0 1 0 1 1 1 1 0 1 0 0 1 1 1 0 0 0 1 0 0 0 1 0 0 1 1 0 0 1 1
1 0 1 1 1 1 1 1 0 1 0 0 1 1 0 1 0 0 0 0 0 1 1 0 1 1]
4.2 第2步:
Alice随机地用 Z 基和 X 基对这些比特进行编码,并通过Eve的量子信道将它们发送给Bob:
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
## Step 2
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
print(alice_bases)
[1 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 1 1 0 0
1 1 0 0 0 0 0 0 0 0 1 1 0 0 0 1 0 1 1 1 0 0 1 0 1 0 1 1 0 0 1 0 0 1 1 1 1
1 0 0 0 0 0 1 1 1 0 0 0 0 0 0 1 0 1 0 0 0 1 0 1 1 1]
在这种情况下,Alice消息中的第一个量子比特处于状态 |+\rangle :
message[0].draw()
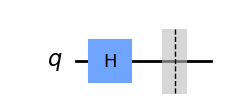
Eve在消息通过她的信道时对其进行了拦截。她试图用随机选择的基测量这些量子比特,就像Bob稍后会做的那样。
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
## Step 2
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Interception!!
eve_bases = randint(2, size=n)
intercepted_message = measure_message(message, eve_bases)
print(intercepted_message)
[1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0]
我们可以看到第0个量子比特的情况:Eve随机选择的基与Alice的不同,这将使量子比特状态从 |+\rangle 变为 Z 基上的随机状态,有50%的概率为 |0\rangle 或 |1\rangle :
message[0].draw()
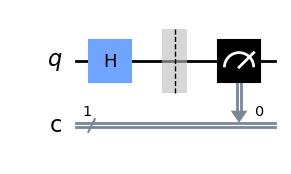
4.3 第3步:
然后Eve将量子比特传递给Bob,Bob随机测量它们。在这种情况下,Bob(碰巧)选择用与Alice准备该量子比特相同的基进行测量。如果没有拦截,Bob必然会测得0,但由于Eve试图读取消息,他现在有50%的概率测得1。
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
## Step 2
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Interception!!
eve_bases = randint(2, size=n)
intercepted_message = measure_message(message, eve_bases)
## Step 3
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
message[0].draw()
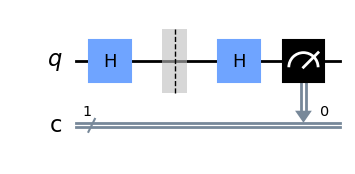
4.4 第4步:
Bob和Alice公开他们的基选择,并丢弃无用的比特:
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
## Step 2
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Interception!!
eve_bases = randint(2, size=n)
intercepted_message = measure_message(message, eve_bases)
## Step 3
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
## Step 4
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
4.5 第5步:
Bob和Alice比较他们密钥中相同的随机选择,看看量子比特是否被拦截:
np.random.seed(seed=3)
## Step 1
alice_bits = randint(2, size=n)
## Step 2
alice_bases = randint(2, size=n)
message = encode_message(alice_bits, alice_bases)
## Interception!!
eve_bases = randint(2, size=n)
intercepted_message = measure_message(message, eve_bases)
## Step 3
bob_bases = randint(2, size=n)
bob_results = measure_message(message, bob_bases)
## Step 4
bob_key = remove_garbage(alice_bases, bob_bases, bob_results)
alice_key = remove_garbage(alice_bases, bob_bases, alice_bits)
## Step 5
sample_size = 15
bit_selection = randint(n, size=sample_size)
bob_sample = sample_bits(bob_key, bit_selection)
print(" bob_sample = " + str(bob_sample))
alice_sample = sample_bits(alice_key, bit_selection)
print("alice_sample = "+ str(alice_sample))
bob_sample = [1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0]
alice_sample = [1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0]
bob_sample == alice_sample
False
Bob的密钥和Alice的密钥不匹配。我们知道这是因为Eve在第2步和第3步之间试图读取消息,改变了量子比特的状态。就Alice和Bob而言,这可能是由于信道中的噪声造成的,但无论如何,他们都必须丢弃所有结果并重试——Eve的拦截企图失败了。
5. 风险分析
对于这种Eve测量所有量子比特的拦截类型,Bob和Alice的样本有很小的概率匹配,Alice通过Eve的信道发送她的易受攻击的消息。让我们计算这种概率,看看量子密钥分发的风险有多大。
- 要让Alice和Bob使用一个量子比特的结果,他们必须都选择相同的基。如果Eve也选择了这个基,她将成功拦截这个比特而不引入任何错误。这种情况发生的概率为50%。
- 如果Eve选择了错误的基,即与Alice和Bob不同的基,Bob仍有50%的概率测量到Alice试图发送的值。在这种情况下,拦截也不会被发现。
- 但如果Eve选择了错误的基,即与Alice和Bob不同的基,Bob有50%的概率不会测量到Alice试图发送的值,这将在他们的密钥中引入一个错误。
如果Alice和Bob比较他们密钥中的1个比特,比特匹配的概率为0.75,这样他们就不会注意到Eve的拦截。如果他们测量2个比特,拦截不被发现的概率为 0.75^2 = 0.5625 。我们可以看到,根据爱丽丝和鲍勃选择比较的比特数(x),可以计算出Eve不被发现的概率:
P(不被发现) = 0.75^x
如果我们决定像上面那样比较15个比特,Eve不被发现的概率为1.3%。如果这对我们来说风险太大,我们可以比较50个比特,有0.00006%的概率在不知情的情况下被监听。


