![]()
量子游走搜索算法
量子游走是经典马尔可夫链的量子等价物,它已成为许多量子算法的关键组成部分。本节我们将实现一个量子游走搜索算法,用于在图中寻找标记元素。与经典算法相比,该算法具有二次加速的优势。
1. 经典马尔可夫链
马尔可夫链是一种随机过程,通常用于对现实生活中的过程进行建模。它由状态和相关的转移概率组成,转移概率描述了在每个时间步长内在状态之间移动的概率。在我们这里使用的离散时间马尔可夫链中,时间步长是离散的。马尔可夫链满足马尔可夫性质,这意味着过程的下一步只取决于当前步骤,而不取决于之前的任何步骤。马尔可夫链有一个相关的转移矩阵P,描述了在每个状态之间移动的概率。下面我们展示了一个马尔可夫链及其相关转移矩阵P的示例。
P = \begin{pmatrix}
0.1&0.3&0.3 \\
0.1&0.1&0.2 \\
0.8&0.6&0.5
\end{pmatrix}
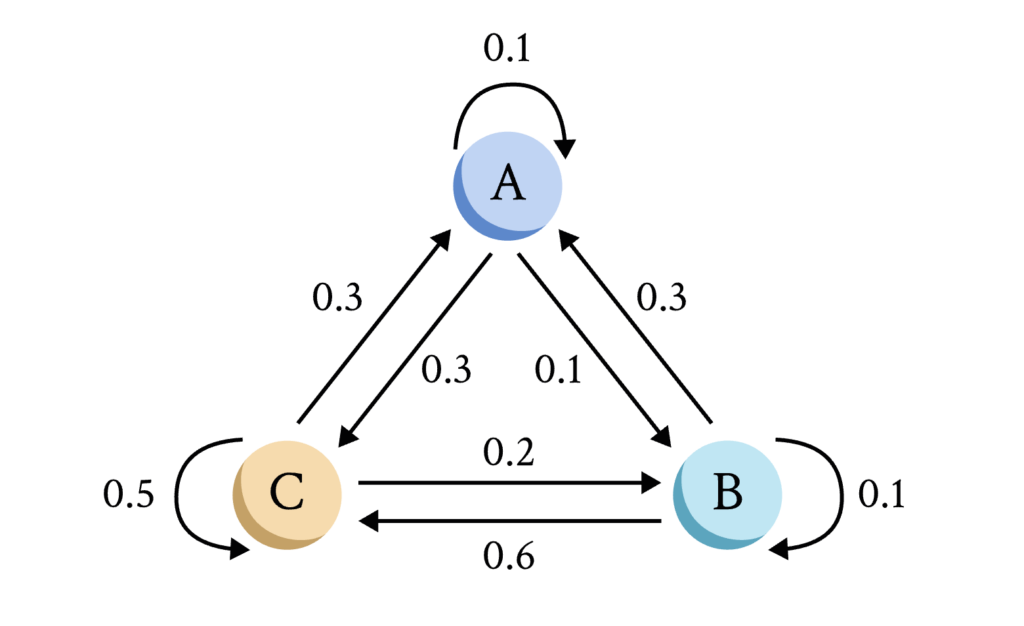
给定转移矩阵P,我们可以通过 P^t 获得t个时间步长后的概率分布。
2. 量子游走
量子游走是经典马尔可夫链的量子等价物。由于叠加态的存在,量子游走将同时走过所有可能的路径,直到我们对线路进行测量。由于量子干涉,一些状态将被抵消。这使得量子游走算法比经典算法更快,因为我们可以设计它们,使错误答案快速抵消。量子游走有两种常见的模型:硬币式量子游走和Szegedy量子游走,它们在某些情况下是等价的。硬币式量子游走发生在图的顶点上,而Szegedy量子游走发生在边上。在展示如何实现量子游走之前,我们将介绍这两种模型。
2.1 硬币式量子游走
硬币式量子游走的一个简单示例是在无限整数线上的游走。在这种情况下,我们用一个整数 {|j\rangle : j \in \mathbb{Z} } 来表示游走者的位置,因为游走者可以走遍 \mathbb{Z} 中的所有整数。我们可以用一枚硬币决定游走者应该如何移动。在整数线上,游走者可以向左或向右移动。因此,硬币的计算基础是 {|0\rangle, |1\rangle} ,如果硬币是 |0\rangle ,我们将游走者向一个方向移动,如果硬币是 |1\rangle ,则向另一个方向移动。
硬币式量子游走是在图节点上的游走,我们将节点称为状态。游走者可以在由边连接的状态之间移动。在硬币模型中,我们有两个量子态和两个算符。第一个状态是位置状态,表示游走者的位置,游走者可以位于整数线上的任何整数位置。另一个状态是硬币状态。硬币状态决定游走者在下一步中应该如何移动。我们可以用Hilbert空间中的向量来表示硬币状态和位置状态。如果我们可以用 \mathcal{H}_ C 中的向量表示硬币状态,用 \mathcal{H}_ P 中的向量表示位置状态,那么我们可以将整个游走者的量子空间表示为 \mathcal{H} = \mathcal{H}_ C \otimes \mathcal{H}_ P 。
如前所述,该模型还有两个算符:硬币算符C和移位算符S。硬币算符在每个时间步长内作用于 \mathcal{H}_ C ,使游走者进入叠加态,从而同时走过所有可能的路径。对于整数线上的游走,这意味着它在每个时间步长内既向左移动又向右移动。有不同的硬币算符,但最常见的是Hadamard硬币和Grover硬币。Hadamard硬币是一个Hadamard门,它使游走者处于相等的叠加态:
H = \frac{1}{\sqrt{2}}
\begin{bmatrix}
1&1 \\
1&-1
\end{bmatrix}
Grover硬币是来自Grover算法的Grover扩散算符。我们将其定义为
G =
\begin{bmatrix}
\frac{2}{n} -1&\frac{2}{n}&\ldots&\frac{2}{n}\\
\frac{2}{n}&\frac{2}{n} – 1&\ldots &\frac{2}{n} \\
\vdots&\vdots&\ddots&\vdots \\
\frac{2}{n}&\frac{2}{n}&\ldots&\frac{2}{n} -1
\end{bmatrix}
与Hadamard硬币一样,Grover硬币也使游走者进入叠加态。但是,它的行为有点不同。如果我们将Grover硬币应用于位置 |000\rangle 的游走者,硬币没有像Hadamard硬币那样使游走者处于相等的叠加态。相反, |000\rangle 的概率远大于其他状态。
该模型中的另一个算符,移位算符作用于 \mathcal{H}_ P ,将游走者移动到下一个位置。对于整数线上的游走,如果硬币为 |0\rangle ,移位算符将游走者向左移动,如果硬币为 |1\rangle ,则向右移动:
S |0\rangle|j\rangle = |0\rangle|j+1\rangle
S |1\rangle|j\rangle = |1\rangle|j-1\rangle
定义了上述移位算符后,我们可以将硬币式量子游走的一步表示为幺正算符 U,其中
U = SC,
其中C是硬币算符。对于整数线上的量子游走,我们使用Hadamard硬币,但C可以是Hadamard硬币、Grover硬币或任何其他硬币算符。
我们还可以展望几步。我们可以将t个时间步长后的量子态 |\psi\rangle 表示为
|\psi (t)\rangle = U^t |\psi(0)\rangle,
其中 |\psi(0)\rangle 是初始状态, U 是游走一步的算符[1]。
硬币式量子游走最适合于正则图,即所有节点都具有相同数量邻居的图[2]。另一种更适合非正则图的量子游走模型是我们接下来要看的Szegedy模型。
2.2 Szedgedy量子游走
与基于硬币的量子游走在图的节点上进行不同,Szegedy量子游走是基于图的边的,是一种离散时间量子游走模型,但不依赖于硬币操作。为了构建这个模型,我们从经典游走的转移概率矩阵P开始。我们用转移矩阵P来表示经典的离散时间随机游走。对于任何具有 N \times N 转移矩阵P的N个节点的图,我们可以将相应的离散时间量子游走定义为希尔伯特空间 \mathcal{H}^N \otimes \mathcal{H}^N 上的幺正算符。设 P_{jk} 表示从状态 j 转移到 k 的概率。在定义游走之前,我们先定义归一化状态
以及到 {|\psi_j\rangle}:j=1,…,N 上的投影
\Pi := \sum_{j=1}^N |\psi_j\rangle \langle \psi_j|
我们还引入了移位算符S:
S := \sum_{j,k=1}^N |j,k\rangle \langle k,j|
根据上面定义的 S 和 \Pi ,我们可以给出离散时间量子游走的一步演化:
U := S(2 \Pi – 1),
其中 (2 \Pi – 1) 是反射算符。我们还将 t 步游走定义为 U^t [2]。
3. 示例:在超立方体上实现量子游走
超立方体是3维立方体在 n 维空间的推广。所有节点的度为 n ,超立方体总共有 N=2^n 个节点。我们可以用二进制数的 n 元组来表示超立方体图中的节点。一个节点的邻居节点的二进制表示只会有一位不同。例如,在4维超立方体中, 0000 的邻居是 0001 、 0010 、 0100 和 1000 。因此,一个节点与所有到它的汉明距离为1的节点相连。边也是有标号的。两个相邻节点在第 a 位上不同,它们之间的边就标号为 a 。
表示超立方体上基于硬币的量子游走的希尔伯特空间是 \mathcal{H} = \mathcal{H}^n \otimes \mathcal{H}^{2^n} ,其中 \mathcal{H}^n 表示硬币空间, \mathcal{H}^{2^n} 表示行走者的位置。计算基为
|a,\vec{v}\rangle, 0 \leq a \leq n-1,
硬币计算基 a 的值与边 a 相关联,它决定了行走者应该移动到哪里。如果 a=0 ,行走者将移动到第一个二进制值与当前节点不同的节点。如果 a=1 ,行走者将移动到第二个值与当前值不同的节点,以此类推。设 \vec{e}_ a 为一个 n 元组,除了索引为 a 的值之外,其他所有二进制值都为 0 。则移位算符 S 将行走者从状态 |a\rangle |\vec{v}\rangle 移动到 |\vec{v} \oplus \vec{e}_ a\rangle :
S |a\rangle |\vec{v}\rangle = |a\rangle |\vec{v} \oplus \vec{e}_ a\rangle.
我们在这个游走中使用Grover硬币 G 。因此,演化算符为
U = SG.
下面我们将展示如何在4维超立方体上实现量子游走。我们需要实现硬币算符和移位算符。
import deepquantum as dq
cir = dq.QubitCircuit(6)
cir.h(4)
cir.h(5)
cir.z(4)
cir.z(5)
cir.cz(4,5)
cir.h(4)
cir.h(5)
cir.draw()
c:\Users\HP\.conda\envs\dq\lib\site-packages\qiskit\visualization\circuit\matplotlib.py:266: FutureWarning: The default matplotlib drawer scheme will be changed to "iqp" in a following release. To silence this warning, specify the current default explicitly as style="clifford", or the new default as style="iqp".
self._style, def_font_ratio = load_style(self._style)
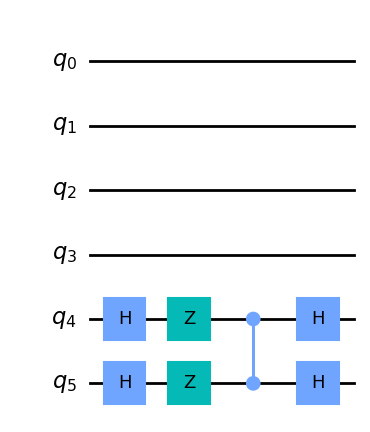
量子线路将有6个量子比特,4个表示位置,2个表示硬币。如前所述,硬币是Grover硬币,它是Grover算法中的扩散器。我们首先来实现它。
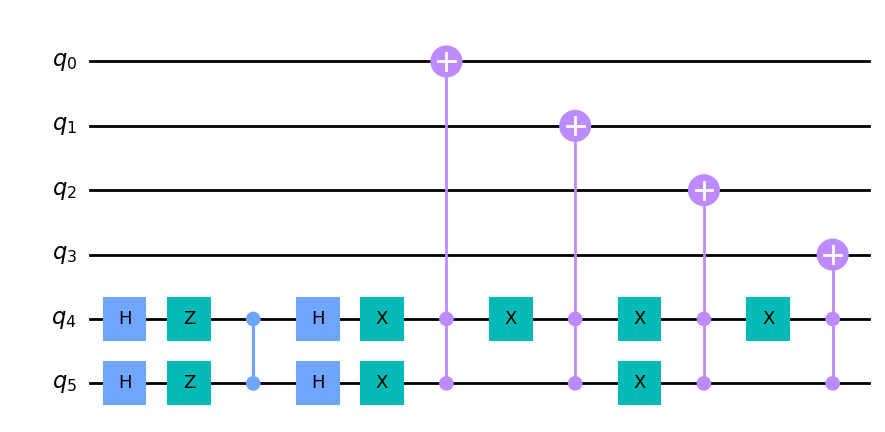
现在,让我们来实现移位算符。我们知道行走者只能移动到相邻节点,所有相邻节点只有一个比特不同。我们希望根据硬币来移动行走者,通过对节点量子比特之一应用非门来移动行走者。如果硬币处于状态 |11\rangle ,我们将行走者移动到第一个节点量子比特不同的状态。如果硬币是 |10\rangle 或 |01\rangle ,行走者分别移动到第二个和第三个量子比特不同的状态。最后,如果Grover硬币是 |00\rangle ,我们翻转第四个量子比特。我们在Grover硬币之后用CCNOT门和非门来实现这一点。它们一起构成了4维超立方体上量子游走的一步。
cir = dq.QubitCircuit(6)
cir.h(4)
cir.h(5)
cir.z(4)
cir.z(5)
cir.cz(4,5)
cir.h(4)
cir.h(5)
for i in range(0,4):
cir.x(4)
if i%2==0:
cir.x(5)
cir.ccx(4,5,i)
cir.draw()
4. 量子游走搜索算法
现在我们将实现一个量子游走搜索算法来寻找图中的标记顶点。我们标记某些顶点集合 |M| ,从图中任意一个节点开始,根据游走规则移动直到找到标记节点。量子游走搜索算法中的基态有两个寄存器,一个对应当前节点,另一个对应前一个节点。也就是说,基态对应于图中的边。我们用幺正算符 W(P) 表示基于经典马尔可夫链转移矩阵 P 的量子游走在 \mathcal{H} 上的演化。我们还定义 |p_x\rangle = \sum_y \sqrt{P_{xy}}|y\rangle 为节点 x 的邻居上的均匀叠加态。设 |x\rangle|y\rangle 为一个基态。如果 x 是标记节点,我们称基态 |x\rangle|y\rangle 为”好”的基态,否则称其为”坏”的基态。现在我们引入”好”态和”坏”态:
它们分别是好的基态和坏的基态的叠加态。接下来,定义 \epsilon = |M|/N 和 \theta = \arcsin(\sqrt{\epsilon})。
简而言之,该算法由三个步骤组成:
- 设置初始态 |U\rangle = \frac{1}{\sqrt{N}} \sum_{x} |x\rangle |p_x\rangle = \sin{\theta} |G\rangle + \cos{\theta} |B\rangle ,即所有边上的均匀叠加态
- 重复 O(1/\sqrt{\epsilon}) 次:
(a) 关于 |B\rangle 反射
(b) 关于 |U\rangle 反射
-
在计算基上做测量,我们可以用Hadamard门轻松实现第1步,用相位算符实现关于 |B\rangle 的反射,它在 x 在第一个寄存器中时改变 x 的相位,否则线路保持不变。
步骤2(b)等价于找到一个幺正算符 R(P) ,执行以下映射:
|U\rangle \mapsto |U\rangle,
|\psi\rangle \mapsto -|\psi\rangle,
为了找到这个算符,我们对 W(P) 应用相位估计。前面我们将 W(P) 定义为随机游走的演化算符, W(P) 的本征值模为 1 。因此,我们可以将 W(P) 的本征值写成 e^{\pm 2i\theta_j} 的形式。幺正算符 W(P) 有一个本征向量,相应的本征值为 1 ,即 |U\rangle 。这由 \theta_1=0 给出。 R(P) 将通过增加一个含有辅助量子比特的寄存器并以 O(1/\sqrt{\delta}) 的精度执行相位估计来找到这个向量 |U\rangle ,其中 \delta 是 P 的谱间隙。为此,我们需要应用 W(P) O(1/\sqrt{\delta}) 次。设 |w\rangle 是 W(P) 的本征向量,相应的本征值为 e^{\pm 2i\theta_j} 。假设 \tilde{\theta_j} 是由相位估计给出的对 \theta_j 的最佳近似。在步骤2(b)中对 |w\rangle 执行映射的算符 R(P) 由下式给出[3]
5. 示例:在4维超立方体上的量子游走搜索
量子游走搜索算法可以在 O(1/\sqrt{\epsilon}) 步内找到一组被标记的节点,\epsilon = |M|/N ,其中 M 是被标记节点的数量, N 是节点总数。该算法最初与 Szegedy 量子游走一起使用,我们使用两个节点寄存器来表示量子态。然而,带有 Grover coin 的 coined 游走等价于 Szegedy 量子游走,而且由于 coined 游走的实现通常更简单,因此我们选择用 coined 游走来实现该算法。我们将使用第 3 节中实现的 4 维超立方体。
我们将按如下方式实现该算法。我们通过对节点量子位和硬币量子位应用 Hadamard 门来实现步骤 1,即在所有边上的均匀叠加。对于步骤 2(a),我们实现一个相位 oracle。步骤 2(b)通过对超立方体上的量子游走的一步执行相位估计来实现,然后标记所有 \theta \neq 0 的量子态。我们通过旋转辅助量子位来实现这一点。在该步骤的最后部分,我们反转相位估计。 theta 量子位的数量取决于 \theta 的精度。
下面,我们在 4 维超立方体上实现量子游走搜索算法。
对于该算法,我们需要使用前面实现的单步门的逆。我们通过使用内置的线路函数 inverse() 来实现这一点。
from typing import Any, List, Optional, Union
import torch
import deepquantum as dq
import numpy as np
class one_step_circuit(dq.Ansatz):
def __init__(
self,
nqubit: int,
minmax: Optional[List[int]] = None,
controls: Union[int, List[int], None]=None,
reverse: bool = False,
init_state: Any = 'zeros',
den_mat: bool = False,
mps: bool = False,
chi: Optional[int] = None,
show_barrier: bool = False
) -> None:
super().__init__(nqubit=nqubit, wires=None, minmax=minmax, ancilla=None, controls=controls,
init_state=init_state, name='one_step_circuit', den_mat=den_mat,
mps=mps, chi=chi)
self.one_step(controls)
def one_step(self,controls):
self.h(self.wires[4],controls=controls)
self.h(self.wires[5],controls=controls)
self.z(self.wires[4],controls=controls)
self.z(self.wires[5],controls=controls)
if controls!=None:
self.z(wires=[self.wires[5]], controls=[controls,self.wires[4]])
else:
self.cz(self.wires[4],self.wires[5])
self.h(self.wires[4],controls=controls)
self.h(self.wires[5],controls=controls)
for i in self.wires[0:4]:
self.x(self.wires[4],controls=controls)
if i%2==0:
self.x(self.wires[5],controls=controls)
if controls!=None:
self.x(wires=i, controls=[controls,self.wires[4],self.wires[5]])
else:
self.ccx(self.wires[4],self.wires[5],i)
cir=one_step_circuit(nqubit=6,minmax=[0, 5])
cir.inverse().draw()
c:\Users\HP\.conda\envs\dq\lib\site-packages\qiskit\visualization\circuit\matplotlib.py:266: FutureWarning: The default matplotlib drawer scheme will be changed to "iqp" in a following release. To silence this warning, specify the current default explicitly as style="clifford", or the new default as style="iqp".
self._style, def_font_ratio = load_style(self._style)
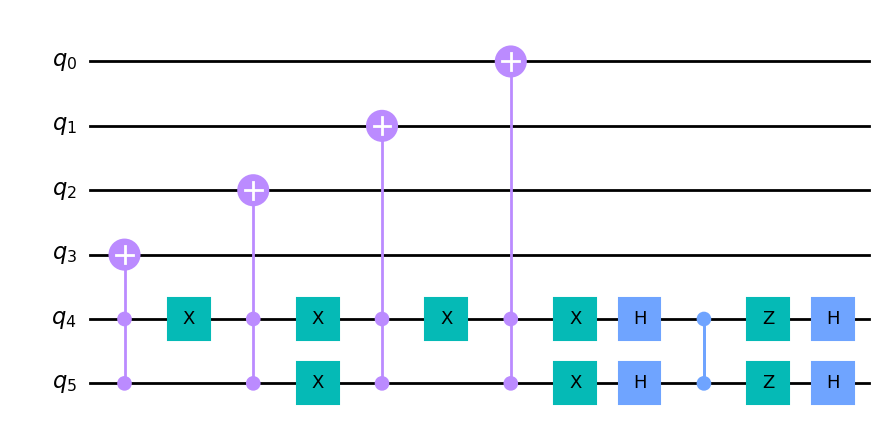
逆转的单步门将用于在稍后反转相位估计。我们需要从第 3 节中实现的单步门及其逆门制作受控门。我们稍后将根据控制量子位的值使用它们。
cir=one_step_circuit(nqubit=8,minmax=[2, 7],controls=0)
cir.inverse().draw()
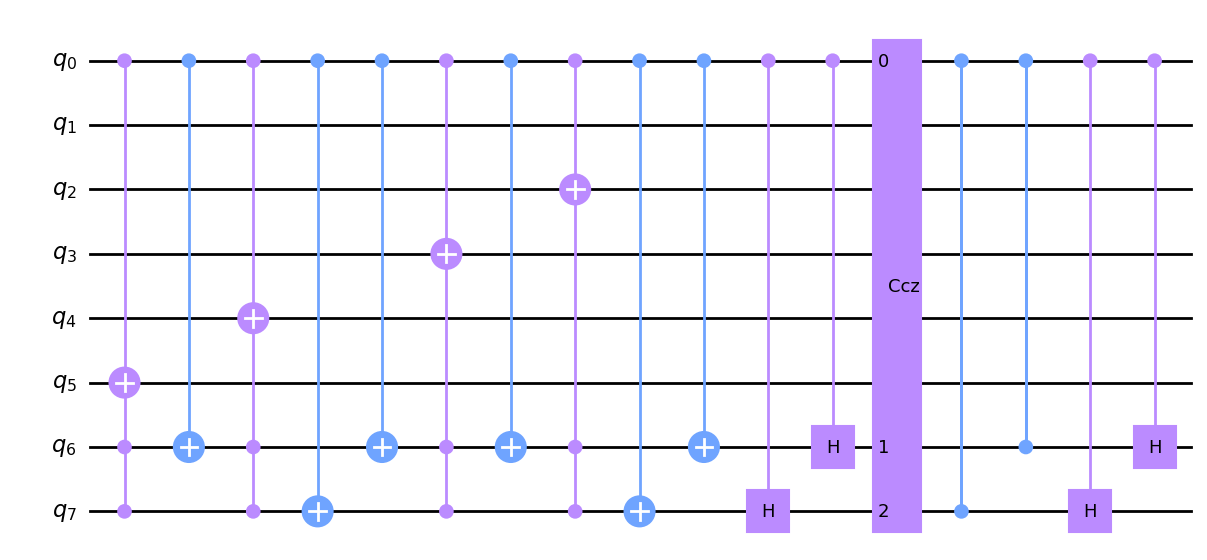
受控单步门和受控逆单步门都将在相位估计中使用。我们将在相位估计中使用量子傅里叶变换。
class QuantumFourierTransform(dq.Ansatz):
def __init__(
self,
nqubit: int,
minmax: Optional[List[int]] = None,
reverse: bool = False,
init_state: Any = 'zeros',
den_mat: bool = False,
mps: bool = False,
chi: Optional[int] = None,
show_barrier: bool = False
) -> None:
super().__init__(nqubit=nqubit, wires=None, minmax=minmax, ancilla=None, controls=None,
init_state=init_state, name='QuantumFourierTransform', den_mat=den_mat,
mps=mps, chi=chi)
self.reverse = reverse
for i in self.wires:
self.qft_block(i)
if show_barrier:
self.barrier(self.wires)
if not reverse:
for i in range(len(self.wires) // 2):
self.swap([self.wires[i], self.wires[-1 - i]])
def qft_block(self, n):
self.h(n)
k = 2
for i in range(n, self.minmax[1]):
self.cp(i + 1, n, torch.pi / 2 ** (k - 1))
k += 1
QuantumFourierTransform(nqubit=4, minmax=[0, 3],reverse=True).inverse().draw()
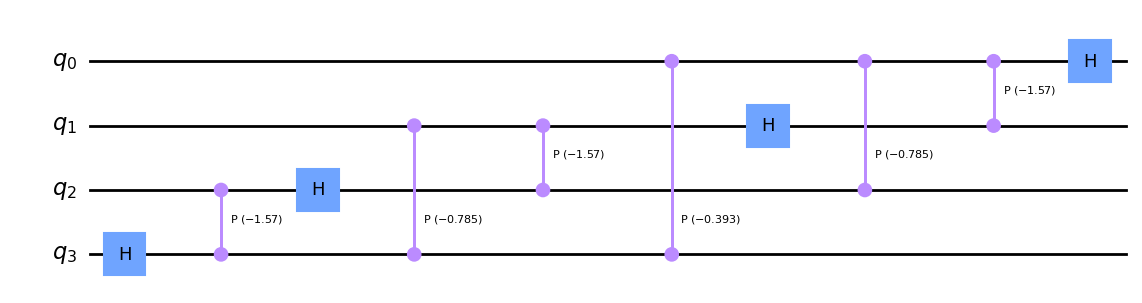
在实现相位估计之前,我们实现一个相位 oracle,用于标记状态 1011 和 1111。然后,我们将其制作成量子线路。这是算法的步骤 2(a)。
class phase_circuit(dq.Ansatz):
def __init__(
self,
nqubit: int,
minmax: Optional[List[int]] = None,
controls: Union[int, List[int], None]=None,
reverse: bool = False,
init_state: Any = 'zeros',
den_mat: bool = False,
mps: bool = False,
chi: Optional[int] = None,
show_barrier: bool = False
) -> None:
super().__init__(nqubit=nqubit, wires=None, minmax=minmax, ancilla=None, controls=controls,
init_state=init_state, name='phase_circuit', den_mat=den_mat,
mps=mps, chi=chi)
# Mark 1011
self.x(self.wires[2])
self.h(self.wires[3])
self.x(self.wires[3],controls=[self.wires[0],self.wires[1],self.wires[2]])
self.h(self.wires[3])
self.x(self.wires[2])
# Mark 1111
self.h(self.wires[3])
self.x(self.wires[3],controls=[self.wires[0],self.wires[1],self.wires[2]])
self.h(self.wires[3])
cir=phase_circuit(nqubit=6, minmax=[0, 5])
cir.draw()
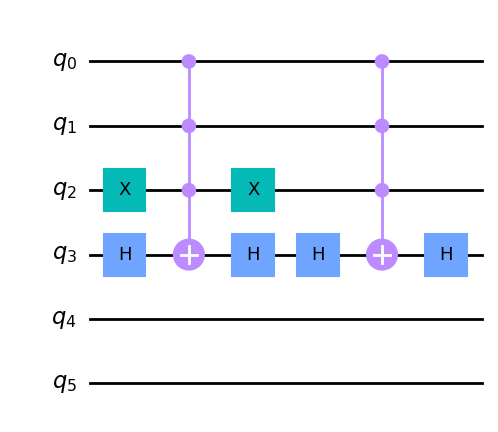
现在,我们将实现一个门,如果其他量子位非零,则旋转辅助量子位。我们将在相位估计中使用此门,如果 \theta \neq 0,它将旋转辅助量子位。
class mark_auxiliary_circuit(dq.Ansatz):
def __init__(
self,
nqubit: int,
minmax: Optional[List[int]] = None,
controls: Union[int, List[int], None]=None,
wires: Union[int, List[int], None]=None,
reverse: bool = False,
init_state: Any = 'zeros',
den_mat: bool = False,
mps: bool = False,
chi: Optional[int] = None,
show_barrier: bool = False
) -> None:
super().__init__(nqubit=nqubit, wires=wires, minmax=minmax, ancilla=None, controls=controls,
init_state=init_state, name='mark_auxiliary_circuit', den_mat=den_mat,
mps=mps, chi=chi)
self.xlayer(wires=[self.wires[0],self.wires[1],self.wires[2],self.wires[3],self.wires[4]])
self.x(self.wires[4],controls=[self.wires[0],self.wires[1],self.wires[2],self.wires[3]])
self.z(self.wires[4])
self.x(self.wires[4],controls=[self.wires[0],self.wires[1],self.wires[2],self.wires[3]])
self.xlayer(wires=[self.wires[0],self.wires[1],self.wires[2],self.wires[3],self.wires[4]])
cir=mark_auxiliary_circuit(nqubit=5, minmax=[0, 4])
cir.draw()
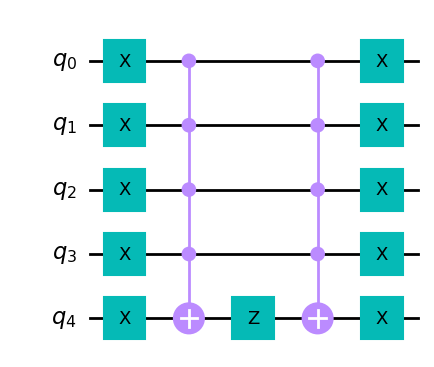
现在,我们将实现算法的步骤 2(b)。该步骤包括量子游走的一步相位估计,然后是一个辅助量子位,如果 \theta \neq 0 我们就旋转它。为此,我们使用刚刚创建的 mark_auxiliary_gate。此后,我们反转相位估计。
class Phase_estimation(dq.Ansatz):
def __init__(
self,
nqubit: int,
minmax: Optional[List[int]] = None,
controls: Union[int, List[int], None]=None,
reverse: bool = False,
init_state: Any = 'zeros',
den_mat: bool = False,
mps: bool = False,
chi: Optional[int] = None,
show_barrier: bool = False
) -> None:
super().__init__(nqubit=nqubit, wires=None, minmax=minmax, ancilla=None, controls=controls,
init_state=init_state, name='Phase_estimation', den_mat=den_mat,
mps=mps, chi=chi)
self.hlayer(wires=[self.wires[0],self.wires[1],self.wires[2],self.wires[3]])
for i in range(0,4):
stop = 2**i
for j in range(0,stop):
self.add(one_step_circuit(nqubit=11,minmax=[4, 9],controls=i))
self.add(QuantumFourierTransform(nqubit=11, minmax=[0, 3],reverse=True).inverse())
self.add(mark_auxiliary_circuit(nqubit=11, wires=[0,1,2,3,10]))
self.add(QuantumFourierTransform(nqubit=11, minmax=[0, 3],reverse=True))
for i in range(3,-1,-1):
stop = 2**i
for j in range(0,stop):
self.add(one_step_circuit(nqubit=11,minmax=[4, 9],controls=i).inverse())
self.barrier()
self.hlayer(wires=[self.wires[0],self.wires[1],self.wires[2],self.wires[3]])
cir=Phase_estimation(nqubit=11, minmax=[0, 10])
现在,我们使用之前制作的门来实现整个量子游走搜索算法。我们首先对节点和硬币量子位应用 Hadamard 门,这是算法中的步骤 1。之后,我们迭代地应用相位 oracle 门和相位估计门(步骤 2(a)和 2(b))。正如算法描述的第 4 节中所述,我们需要 O(1/\sqrt{\epsilon}) 次迭代。最后,我们测量节点量子位。
cir = dq.QubitCircuit(11)
cir.hlayer(wires=[4,5,6,7,8,9])
iterations = 2
for i in range(0,iterations):
cir.add(phase_circuit(nqubit=11, minmax=[4, 9]))
cir.add(Phase_estimation(nqubit=11, minmax=[0, 10]))
cir.measure(wires=[4,5,6,7])
cir.draw()
最后,我们在模拟器上运行实现。我们看到,量子线路在绝大多数情况下会塌缩到标记的状态。
cir()
res=cir.measure(wires=[4,5,6,7])
print(res)
import matplotlib.pyplot as plt
# 准备x轴和y轴的数据
keys = list(res.keys())
values = list(res.values())
# 创建条形图
plt.bar(keys, values)
# 设置图表的标题和轴标签
plt.xlabel('Keys')
plt.ylabel('Values')
# 设置x轴的刻度标签,以便它们更容易阅读
plt.xticks(rotation=90)
# 显示图表
plt.show()
{'1101': 456, '1111': 474, '0011': 2, '1010': 6, '0100': 5, '1000': 10, '0101': 10, '1011': 2, '0010': 12, '0000': 12, '0110': 8, '1001': 4, '0111': 5, '1110': 11, '0001': 2, '1100': 5}

参考文献
[1] Portugal R. Quantum walks and search algorithms[M]. New York: Springer, 2013.
[2] Wanzambi E, Andersson S. Quantum computing: Implementing hitting time for coined quantum walks on regular graphs[J]. arXiv preprint arXiv:2108.02723, 2021.
[3] De Wolf R. Quantum computing: Lecture notes[J]. arXiv preprint arXiv:1907.09415, 2019.


