![]()
量子相位估计
量子相位估计是量子计算中最重要的子程序之一,是许多量子算法的核心组成部分。该算法的目标如下:
给定一个幺正算符 U ,算法估计 U\vert\psi \rangle =e^{\boldsymbol{2\pi i} \theta }|\psi \rangle 中的 \theta 。其中 |\psi\rangle 是特征向量, e^{\boldsymbol{2\pi i}\theta} 是对应的特征值。由于 U 是幺正的,所有特征值的模为1。
算法原理
量子相位估计算法利用相位反冲将 U 的相位(在傅里叶基下)写入计数寄存器的 t 个量子比特。然后使用逆QFT将其从傅里叶基转换到计算基,以便我们可以测量。
如上所述,量子线路估计幺正算符 U 的相位。它估计 U\vert\psi \rangle =e^{\boldsymbol{2\pi i} \theta }|\psi \rangle 中的 \theta ,其中 |\psi\rangle 是特征向量, e^{\boldsymbol{2\pi i}\theta} 是对应的特征值。线路按以下步骤运行:
- 初始化:
\vert\psi\rangle 在一组量子比特寄存器中。另一组 n 个量子比特形成计数寄存器,我们将在其中存储值 2^n\theta :
|\psi_0\rangle = \lvert 0 \rangle^{\otimes n} \lvert \psi \rangle -
叠加态:
对计数寄存器应用 n 比特Hadamard门操作 H^{\otimes n} :
|\psi_1\rangle = {\frac {1}{2^{\frac {n}{2}}}}\left(|0\rangle +|1\rangle \right)^{\otimes n} \lvert \psi \rangle -
受控幺正操作:
我们需要引入受控幺正 CU ,它仅在其对应的控制比特为 |1\rangle 时,在目标寄存器上应用幺正算符 U 。由于 U 是具有特征向量 |\psi\rangle 的幺正算符,使得 U|\psi \rangle =e^{\boldsymbol{2\pi i} \theta }|\psi \rangle ,这意味着:
应用所有 n 个受控操作 CU^{2^j} ,其中 0\leq j\leq n-1 ,并使用关系:
其中 k 表示 n 位二进制数的整数表示。
4. 逆傅里叶变换:
QFT可以将 n 量子比特输入态 \vert x\rangle 映射到输出态
将上面表达式中的 x 替换为 2^n\theta ,正好得到上面步骤2中推导的表达式。因此,为了恢复状态 \vert2^n\theta\rangle ,在辅助寄存器上应用逆傅里叶变换。这样做,我们得到:
- 测量:
上面的表达式在 x = 2^n\theta 附近达到峰值。对于 2^n\theta 为整数的情况,在计算基上测量以很高的概率在辅助寄存器中给出相位:
|\psi_4\rangle = | 2^n \theta \rangle \otimes | \psi \rangle
对于 2^n\theta 不是整数的情况,可以证明上面的表达式仍然在 x = 2^n\theta 附近达到峰值,概率优于 4/\pi^2 \approx 40\% [1]。
示例代码
首先,让我们准备环境,搭建量子电路。
from typing import Any, List, Optional, Union
import torch
import deepquantum as dq
import numpy as np
class QuantumFourierTransform(dq.Ansatz):
def __init__(
self,
nqubit: int,
minmax: Optional[List[int]] = None,
reverse: bool = False,
init_state: Any = 'zeros',
den_mat: bool = False,
mps: bool = False,
chi: Optional[int] = None,
show_barrier: bool = False
) -> None:
super().__init__(nqubit=nqubit, wires=None, minmax=minmax, ancilla=None, controls=None,
init_state=init_state, name='QuantumFourierTransform', den_mat=den_mat,
mps=mps, chi=chi)
self.reverse = reverse
for i in self.wires:
self.qft_block(i)
if show_barrier:
self.barrier(self.wires)
if not reverse:
for i in range(len(self.wires) // 2):
self.swap([self.wires[i], self.wires[-1 - i]])
def qft_block(self, n):
self.h(n)
k = 2
for i in range(n, self.minmax[1]):
self.cp(i + 1, n, torch.pi / 2 ** (k - 1))
k += 1
class QuantumPhaseEstimation(dq.Ansatz):
def __init__(
self,
unitary: Any,
t: int,
t_a: int,
den_mat: bool = False,
mps: bool = False,
chi: Optional[int] = None
) -> None:
self.nqubit = t + t_a
self.unitary=unitary
super().__init__(nqubit=self.nqubit, wires=None, minmax=None, ancilla=None, controls=None,
init_state='zeros', name='QuantumPhaseEstimationQubit', den_mat=den_mat,
mps=mps, chi=chi)
self.hlayer(list(range(t)))
self.barrier()
for i in range(t):
self.any(unitary=np.linalg.matrix_power(self.unitary, 2 ** (t - i)),wires=list(range(t,self.nqubit)), controls=i)
self.barrier()
iqft = QuantumFourierTransform(nqubit=self.nqubit, minmax=[0, t - 1],den_mat=self.den_mat, mps=self.mps, chi=self.chi).inverse()
self.add(iqft)
self.barrier()
self.measure(wires=list(range(t)))
#例子参数:
qubit_measurement_num=4 ##定义测量比特数,测量比特的数量影响测量相位的精度。
qubit_auxiliary_num=2 ##定义辅助比特数,辅助比特的数量对应测量的酉矩阵大小。
phase =0.19 ##定义相位
unitary = [[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,np.exp(1j*torch.pi * phase)]] ##定义被测量的U矩阵,需要为酉矩阵
state=[0,0,0,1] ##定义U矩阵对应的特征向量,2^n维度,n为辅助比特数
qpe = QuantumPhaseEstimation(unitary=unitary,t=qubit_measurement_num, t_a=qubit_auxiliary_num)
state = dq.QubitState(qubit_measurement_num+qubit_auxiliary_num, state=state).state
qpe(state=state)
##测量得到答案
res = qpe.measure(wires=list(range(qubit_measurement_num)))
print(res)
max_key = max(res, key=res.get)
print(max_key)
phase_est = int(max_key, 2) / 2 ** qubit_measurement_num
print('估计相位为:'+str(phase_est))
{'0011': 1020, '0010': 1, '0100': 2, '0111': 1}
0011
估计相位为:0.1875
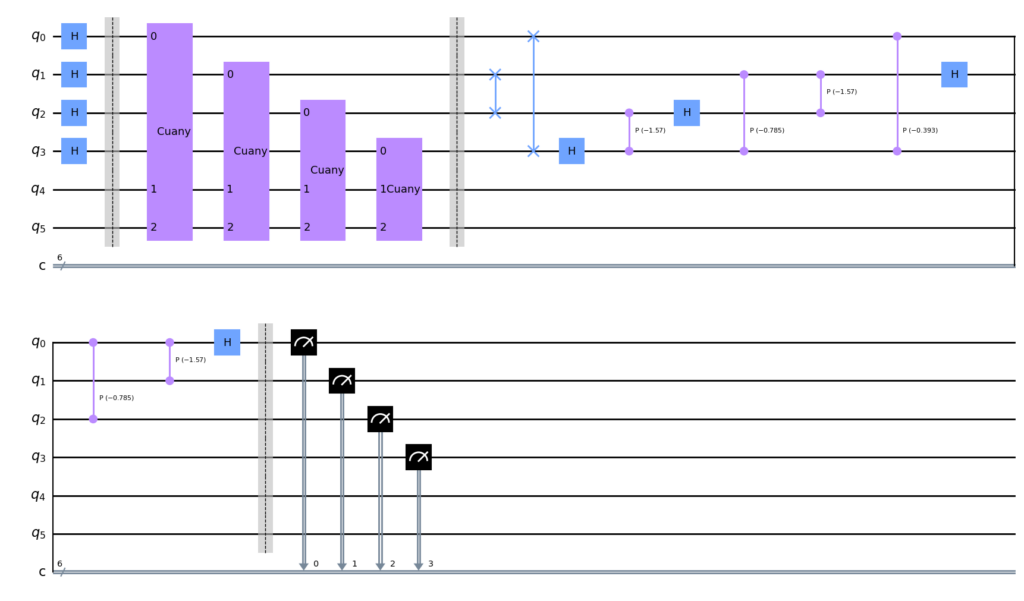
绘制量子相位估计的量子线路
qpe.draw() #绘制量子线路
参考文献
[1] Nielsen M A, Chuang I L. Quantum computation and quantum information[M]. Cambridge university press, 2010.


