![]()
量子迁移学习
简介
迁移学习是一种成熟的人工神经网络训练技术(参见[2])。其基本思路是,如果一个预训练的网络已经能很好地解决一个问题,那么经过少量额外训练,它也可以用来解决一个不同但相关的问题。
正如[1]中所讨论的,这一思想可以用两个抽象网络 A 和 B 来形式化描述,与它们的量子或经典物理本质无关。
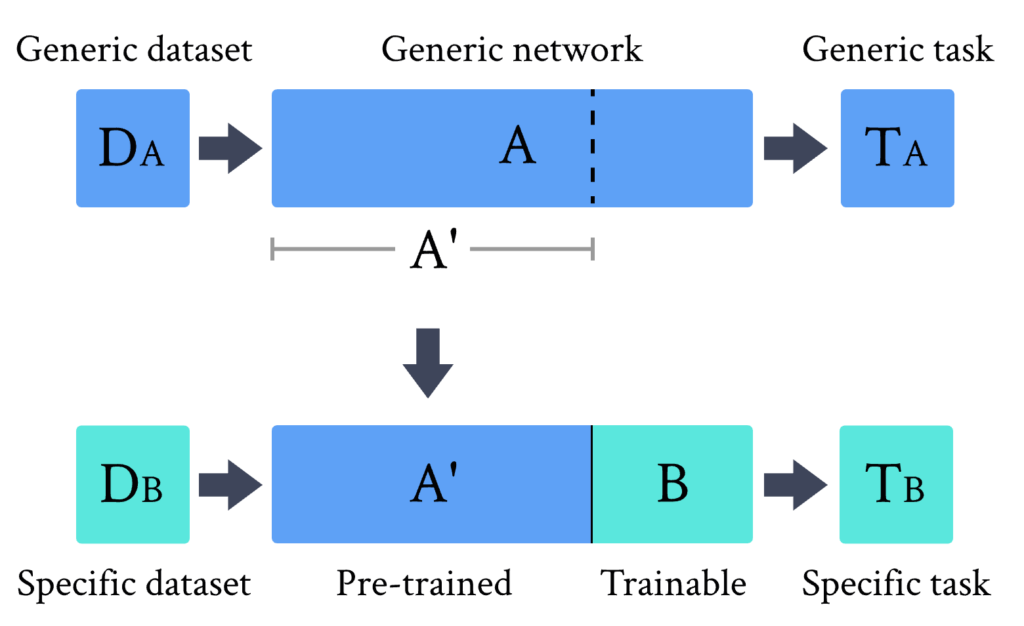
如上图所示,我们可以给出迁移学习方法的一般定义:
- 选取一个在数据集 D_A 上为任务 T_A 预训练过的网络 A 。
- 移除一些末端层。这样截断后的网络 A’ 可以作为特征提取器使用。
- 在预训练网络 A’ 的末端连接一个新的可训练网络 B 。
- 固定 A’ 的权重,用新的数据集 D_B 或感兴趣的新任务 T_B 训练末端模块 B 。
当处理混合系统时,根据网络 A 和 B 的物理性质(经典或量子),可以有不同的迁移学习实现方式,总结如下表:
Network A Network B Transfer learning scheme
经典 经典 CC – Standard classical method. See e.g., Ref.[2].
经典 量子 CQ – Hybrid model presented in this tutorial.
量子 经典 QC – Model studied in Ref. [1].
量子 量子 QQ – Model studied in Ref. [1].
经典-量子迁移学习
我们聚焦于上一节讨论的CQ迁移学习方案,给出一个具体示例。
- 作为预训练网络 A,我们使用ResNet18,这是微软在[3]中提出的一种深度残差神经网络,在 ImageNet 数据集上预训练。
- 移除其最后一层后,我们得到 A’ ,一个将任意高分辨率输入图像映射为512个抽象特征的预处理模块。
- 这些特征由一个4比特的”量子线路” B 进行分类,即夹在两个经典层之间的变分量子线路。
- 保持 A’ 不变,在 Hymenoptera 数据集(ImageNet的一个小子集)上训练该混合模型,其中包含蚂蚁和蜜蜂的图像。
模型主要超参数设置
import time
import os
import copy
import torch
import torch.nn as nn
import torch.optim as optim
from torch.optim import lr_scheduler
import torchvision
from torchvision import datasets, transforms
from torch.utils.data import Dataset, DataLoader
import deepquantum as dq
import numpy as np
import pandas as pd
torch.manual_seed(42)
np.random.seed(42)
import matplotlib.pyplot as plt
from torch.utils.data import Dataset, DataLoader
# OpenMP: 设置并行线程数量
os.environ["OMP_NUM_THREADS"] = "1"
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
n_qubits = 4 # 量子比特数
step = 0.01 # 学习步长
batch_size = 4 # 每次训练的样本数量
num_epochs = 3 # 训练的总轮次
q_depth = 6 # 量子电路的深度(变分层的数量)
gamma_lr_scheduler = 0.1 # 每10个训练周期应用一次的学习率减少比例
q_delta = 0.01 # 量子权重的初始随机扩散
start_time = time.time() # 开始计算的时间
c:\Users\HP\.conda\envs\dq\lib\site-packages\torchvision\io\image.py:13: UserWarning: Failed to load image Python extension: 'Could not find module 'C:\Users\HP\.conda\envs\dq\Lib\site-packages\torchvision\image.pyd' (or one of its dependencies). Try using the full path with constructor syntax.'If you don't plan on using image functionality from `torchvision.io`, you can ignore this warning. Otherwise, there might be something wrong with your environment. Did you have `libjpeg` or `libpng` installed before building `torchvision` from source?
warn(
数据集加载
这是一个非常小的数据集(大约250张图像,包含蚂蚁蜜蜂图像数据集,由于数据集太小而无法从头开始训练经典或量子模型,但在使用迁移学习方法时已经足够了。
PyTorch包torchvision和torch.utils.data用于加载数据集并执行标准的预备图像操作:调整大小、居中、裁剪、归一化等。
# 数据预处理的设置
data_transforms = {
"train": transforms.Compose([
# 若需要数据增强,请取消下列两行的注释
# transforms.RandomResizedCrop(224),
# transforms.RandomHorizontalFlip(),
transforms.Resize(256),
transforms.CenterCrop(224),
transforms.ToTensor(),
# 使用ImageNet的均值和标准差对输入通道进行归一化
transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225]),
]),
"val": transforms.Compose([
transforms.Resize(256),
transforms.CenterCrop(224),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225]),
]),
}
# 数据目录和图片数据集的定义
data_dir = "./hymenoptera_data"
image_datasets = {
"train" if x == "train" else "validation": datasets.ImageFolder(
os.path.join(data_dir, x), data_transforms[x]
)
for x in ["train", "val"]
}
dataset_sizes = {x: len(image_datasets[x]) for x in ["train", "validation"]}
class_names = image_datasets["train"].classes
# 初始化数据加载器
dataloaders = {
x: torch.utils.data.DataLoader(image_datasets[x], batch_size=batch_size, shuffle=True)
for x in ["train", "validation"]
}
# 定义用于展示图片的函数
def imshow(inp, title=None):
"""从张量显示图像。"""
inp = inp.numpy().transpose((1, 2, 0))
# 反向执行最初的归一化操作
mean = np.array([0.485, 0.456, 0.406])
std = np.array([0.229, 0.224, 0.225])
inp = std * inp + mean
inp = np.clip(inp, 0, 1)
plt.imshow(inp)
if title is not None:
plt.title(title)
让我们展示一批测试数据,以对分类问题有个概念。
# 获取一批验证数据
inputs, classes = next(iter(dataloaders["validation"]))
# 将批次数据转换为网格形式
out = torchvision.utils.make_grid(inputs)
# 显示图像网格,并标注各图像对应的类别名称
imshow(out, title=[class_names[x] for x in classes])
# 重新初始化数据加载器
dataloaders = {
x: torch.utils.data.DataLoader(image_datasets[x], batch_size=batch_size, shuffle=True)
for x in ["train", "validation"]
}

变分量子线路
我们首先定义一些构成量子线路的量子层。
现在我们通过DeepQuantum定义量子线路。
其结构是一个典型的变分量子线路:
该模块的输入是一批具有512个实数参数(特征)的向量,输出是一批具有两个实数输出的向量(对应于图像的两个类别:蚂蚁和蜜蜂)。
## 定义VQC模块
class QuLinear(nn.Module):
def __init__(self, input_size, hidden_size):
super(QuLinear, self).__init__()
n_qubits = input_size # 定义比特个数
self.cir = dq.QubitCircuit(n_qubits, reupload=True)
self.cir.hlayer()
self.cir.rylayer(encode=True)
self.cir.rzlayer(encode=True)
self.cir.barrier()
self.cir.cnot_ring()
self.cir.barrier()
self.cir.cnot_ring(step=2)
self.cir.barrier()
self.cir.u3layer()
for i in range(hidden_size): # 以for循环
self.cir.observable(wires=i, basis='z')
def forward(self, x):
ry_parameter = torch.arctan(x) # 将经典数据转化为对应ry的角度
rz_parameter = torch.arctan(x * x) # 将经典数据转化为对应rz的角度
r_parameter = torch.cat([ry_parameter, rz_parameter], dim=1)
self.cir(r_parameter)
return self.cir.expectation()
class QuantumNet(nn.Module):
"""
定义一个名为“QuantumNet”的Torch模块。
"""
def __init__(self):
"""
初始化量子网络的结构。
"""
super().__init__()
self.pre_net = nn.Linear(512, n_qubits) # 将输入特征维度从512降至量子位数
self.Qulinear = QuLinear(n_qubits, n_qubits)
self.post_net = nn.Linear(n_qubits, 2) # 后处理网络,将量子位输出映射到两个输出类别
def forward(self, input_features):
"""
定义输入特征通过“dressed”量子网络的传递方式。
"""
# 使用前处理网络减小特征维度,并将结果缩放到π/2的范围内
pre_out = self.pre_net(input_features)
q_in = torch.tanh(pre_out/10) * np.pi / 2.0
# 为每个批次元素应用量子电路,并收集输出到q_out
q_out = self.Qulinear(q_in)
# 通过后处理网络返回二维预测结果
return self.post_net(q_out)
混合经典-量子模型
我们终于准备好构建完整的混合经典-量子网络了。我们遵循迁移学习的方法:
- 首先从
torchvision.models库中加载经典预训练网络ResNet18。 - 冻结所有权重,因为它们不应该被训练。
- 将最后一个全连接层替换为我们的可训练量子线路。
# 加载预训练权重
weights = torchvision.models.ResNet18_Weights.IMAGENET1K_V1
model_hybrid = torchvision.models.resnet18(weights=weights)
# 冻结模型的所有参数,防止在训练过程中更新
for param in model_hybrid.parameters():
param.requires_grad = False
# 注意,model_hybrid.fc 是 ResNet18 的最后一层
model_hybrid.fc = QuantumNet()
# 根据设备对象选择使用 CUDA 还是 CPU
model_hybrid = model_hybrid.to(device)
训练和结果
在训练网络之前,我们需要指定损失函数。
在分类问题中,我们通常使用交叉熵,它可以直接在torch.nn中获得。
criterion = nn.CrossEntropyLoss()
我们还初始化了Adam优化器,它在每个训练步骤都会被调用以更新模型的权重。
optimizer_hybrid = optim.Adam(model_hybrid.fc.parameters(), lr=step)
我们计划每10个epoch将学习率降低gamma_lr_scheduler倍。
exp_lr_scheduler = lr_scheduler.StepLR(
optimizer_hybrid, step_size=10, gamma=gamma_lr_scheduler
)
接下来是一个稍后将被调用的训练函数。该函数应返回一个经过训练的模型,可用于进行预测(分类)。
我们准备执行实际的训练过程。
def train_model(model, criterion, optimizer, scheduler, num_epochs):
since = time.time()
best_model_wts = copy.deepcopy(model.state_dict())
best_acc = 0.0
best_loss = 10000.0 # 初始化最佳损失为一个较大的数值
best_acc_train = 0.0
best_loss_train = 10000.0 # 初始化训练过程中的最佳损失为一个较大的数值
print("Training started:")
for epoch in range(num_epochs):
# 每个epoch都有训练和验证两个阶段
for phase in ["train", "validation"]:
if phase == "train":
model.train() # 设置模型为训练模式
else:
model.eval() # 设置模型为评估模式
running_loss = 0.0
running_corrects = 0
# 遍历数据
n_batches = dataset_sizes[phase] // batch_size
it = 0
for inputs, labels in dataloaders[phase]:
since_batch = time.time()
batch_size_ = len(inputs)
inputs = inputs.to(device)
labels = labels.to(device)
optimizer.zero_grad()
# 在训练阶段计算梯度并进行优化
with torch.set_grad_enabled(phase == "train"):
outputs = model(inputs)
_, preds = torch.max(outputs, 1)
loss = criterion(outputs, labels)
if phase == "train":
loss.backward()
optimizer.step()
# 打印批处理结果
running_loss += loss.item() * batch_size_
batch_corrects = torch.sum(preds == labels.data).item()
running_corrects += batch_corrects
print(
f"Phase: {phase} Epoch: {epoch+1}/{num_epochs} Iter: {it+1}/{n_batches+1} Batch time: {time.time() - since_batch:.4f}",
end="\r",
flush=True,
)
it += 1
# 打印每个epoch的结果
epoch_loss = running_loss / dataset_sizes[phase]
epoch_acc = running_corrects / dataset_sizes[phase]
print(
f"Phase: {'train' if phase == 'train' else 'validation '} Epoch: {epoch+1}/{num_epochs} Loss: {epoch_loss:.4f} Acc: {epoch_acc:.4f} "
)
# 更新最佳模型(基于验证准确率和损失)
if phase == "validation":
if epoch_acc > best_acc:
best_acc = epoch_acc
best_model_wts = copy.deepcopy(model.state_dict())
if epoch_loss < best_loss:
best_loss = epoch_loss
if phase == "train":
if epoch_acc > best_acc_train:
best_acc_train = epoch_acc
if epoch_loss < best_loss_train:
best_loss_train = epoch_loss
# 更新学习率
if phase == "train":
scheduler.step()
# 打印最终结果
model.load_state_dict(best_model_wts)
time_elapsed = time.time() - since
print(
f"Training completed in {time_elapsed // 60:.0f}m {time_elapsed % 60:.0f}s"
)
print(f"Best validation loss: {best_loss:.4f} | Best validation accuracy: {best_acc:.4f}")
return model
model_hybrid = train_model(
model_hybrid, criterion, optimizer_hybrid, exp_lr_scheduler, num_epochs=num_epochs
)
Training started:
Phase: train Epoch: 1/3 Loss: 0.5802 Acc: 0.7131
Phase: validation Epoch: 1/3 Loss: 0.3311 Acc: 0.9216
Phase: train Epoch: 2/3 Loss: 0.4170 Acc: 0.8402
Phase: validation Epoch: 2/3 Loss: 0.2064 Acc: 0.9477
Phase: train Epoch: 3/3 Loss: 0.3389 Acc: 0.8566
Phase: validation Epoch: 3/3 Loss: 0.1910 Acc: 0.9542
Training completed in 0m 36s
Best validation loss: 0.1910 | Best validation accuracy: 0.9542
可视化模型预测
我们首先为一批测试数据定义一个可视化函数。
def visualize_model(model, num_images=6, fig_name="Predictions"):
images_so_far = 0
_fig = plt.figure(fig_name)
model.eval()
with torch.no_grad():
for _i, (inputs, labels) in enumerate(dataloaders["validation"]):
inputs = inputs.to(device)
labels = labels.to(device)
outputs = model(inputs)
_, preds = torch.max(outputs, 1)
for j in range(inputs.size()[0]):
images_so_far += 1
ax = plt.subplot(num_images // 2, 2, images_so_far)
ax.axis("off")
ax.set_title("[{}]".format(class_names[preds[j]]))
imshow(inputs.cpu().data[j])
if images_so_far == num_images:
return
最后,我们可以运行前面的函数,查看一批图像及其对应的预测。
visualize_model(model_hybrid, num_images=batch_size)
plt.show()

参考文献
[1] Mari A, Bromley T R, Izaac J, et al. Transfer learning in hybrid classical-quantum neural networks[J]. Quantum, 2020, 4: 340.
[2] Raina R, Battle A, Lee H, et al. Self-taught learning: transfer learning from unlabeled data[C]//Proceedings of the 24th international conference on Machine learning. 2007: 759-766.
[3] He K, Zhang X, Ren S, et al. Deep residual learning for image recognition[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 770-778.


