Bernstein-Vazirani算法

Bernstein-Vazirani算法是由Ethan Bernstein和Umesh Vazirani开发的量子算法 [1]。它是最早展示量子计算机相对于传统计算机具有指数级优势的例子之一。在本节中，我们将理解他们解决的问题。

假设有一个我们试图学习的隐藏比特串”a”，并且我们可以访问实现以下标量积的函数 f(\vec{x}) ：

f(\vec{x}) := \vec{a}\cdot\vec{x} \pmod 2,

其中 \vec{a}=(a_0,a_1,…,a_{n-1}) 和 \vec{x}=(x_0,x_1,…,x_{n-1}) 是长度为 n 的比特串，满足 a_i, x_i \in {0,1} 。我们的挑战是通过使用函数 f 来发现 \vec{a} 的隐藏值。我们对 \vec{a} 一无所知，因此唯一能做的就是在不同的点 \vec{x} 处评估 f ，以期获得隐藏的信息。

举个例子，假设我们取 \vec{x}=(1,0,1) 并得到 f(\vec{x}) = 0 。虽然可能不太明显，但知道 f 的结构，这给了我们一些关于 \vec{a} 的信息。在这种情况下， a_0 和 a_2 具有相同的值。这是因为对于该 \vec{x} 值，函数将等价于 a_0 + a_2 \pmod 2 ，只有当它们相等时才会取值为0。

在经典计算中，最优解只需要调用函数 n 次就能确定 \vec{a} ，知道 \vec{a} 和 \vec{x} 的形式，我们可以将 f 重写为：

f(\vec{x})=\sum_{i=0}^{n-1}a_ix_i \pmod 2.

策略是用每次调用函数推断出 \vec{a} 的一个元素。假设我们要确定值 a_i 。我们可以简单地选择 \vec{x} 为除第 i 个位置为1之外的全零向量，因为在这种情况下：

因此，很容易看出需要 n 次 f 的计算。

问题是：我们能用量子计算机更有效地实现吗？答案是肯定的，事实上，我们只需要调用一次函数!

第一步是看看我们如何在线路中表示这个语句。在这种情况下，我们假设有一个Oracle U_f对函数进行编码。

一般来说， U_f 将状态 |\vec{x} \rangle |y\rangle 映射到状态 | \vec{x} \rangle |y + \vec{a} \cdot \vec{x} \pmod{2} \rangle 。

例如，假设 \vec{a}=[0,1,0] 。那么 U_f|111\rangle |0\rangle = |111\rangle|1\rangle ，因为我们在点 \vec{x} = [1,1,1] 处评估 f 。两个值之间的标量积是 1 ，因此输出的最后一个量子比特将取值为 1 。

Bernstein-Vazirani算法根据以下线路利用此Oracle：

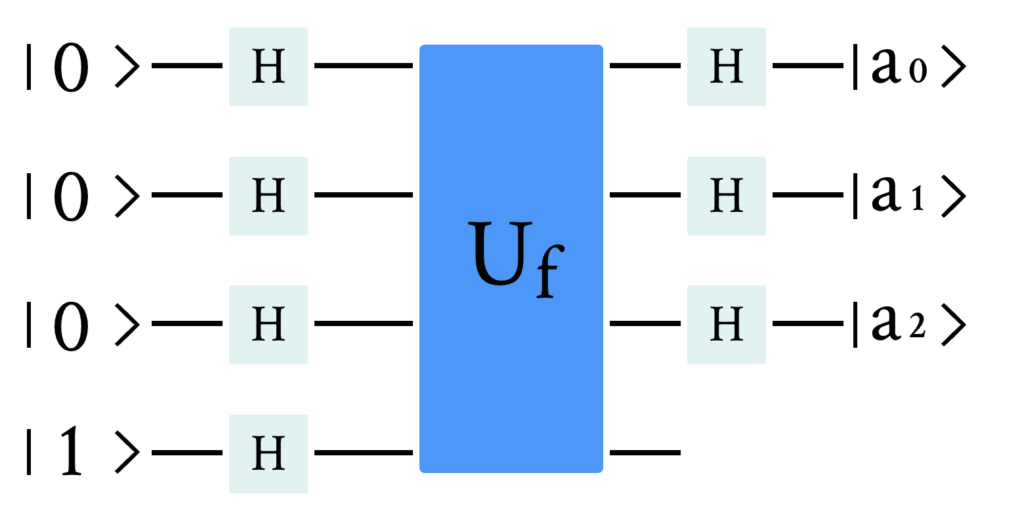
我们可以看到，仅通过在Oracle之前和之后使用Hadamard门，在单次运行后，线路的输出正好是隐藏值 \vec{a} 。让我们做一些数学计算来验证确实如此。

首先，我们线路的输入是 |0001\rangle 。第二步是对这个状态应用Hadamard门，为此我们必须使用以下性质：

H^{\otimes n}|\vec{x}\rangle = \frac{1}{\sqrt{2^n}}\sum_{\vec{z} \in {0,1}^n}(-1)^{\vec{x}\cdot\vec{z}}|\vec{z}\rangle.

以 |0001\rangle 为输入，我们得到状态

为了清晰起见，我们将前三个量子比特与第四个量子比特分开。如果我们现在应用算符 U_f ，

根据 f(\vec{x}) 的值，表达式的最后一部分可以取两个值，可以验证

这是因为，如果 \vec{a}\cdot\vec{z} 取值为 0 ，我们将得到 \frac{|0\rangle – |1\rangle}{\sqrt{2}} ，如果取值为 1 ，结果将是 \frac{|1\rangle – |0\rangle}{\sqrt{2}} = – \frac{|0\rangle – |1\rangle}{\sqrt{2}} 。因此，通过计算 (-1)^{\vec{a}\cdot\vec{z}} 我们涵盖了两种情况。在此之后，我们可以将 (-1)^{\vec{a}\cdot\vec{z}} 因子包含在 |\vec{z}\rangle 项中，并忽略最后一个量子比特，因为我们不会再使用它：

最后，我们将重新应用第一步的性质来计算使用Hadamard后的结果：

重新排列这个表达式，我们得到：

事实上，前面的状态正好是 |\vec{a}\rangle 。你通过证明 \langle \vec{a}|\phi_3\rangle = 1 来演示它。

代码实现

我们首先编写经典解法。我们将在基于DeepQuantum的量子线路中实现它，以理解如何使用 oracle。

import deepquantum as dq

def Uf(cir):
    # 负责编码一个隐藏的“a”值的Oracle。
    cir.cnot(1, 3)
    cir.cnot(2, 3)

    return cir

def circuit0():
    # 用于导出 a0 的电路
    cir = dq.QubitCircuit(4)
    # 初始化 x = [1,0,0]
    cir.x(0)

    # 应用我们的 oracle
    Uf(cir)

    # 我们测量最后一个量子比特
    cir()
    return cir.measure(wires=3)

def circuit1():
    # 用于导出 a1 的电路
    cir = dq.QubitCircuit(4)
    # 初始化 x = [0,1,0]
    cir.x(1)

    # 应用我们的 oracle
    Uf(cir)

    # 我们测量最后一个量子比特
    cir()
    return cir.measure(wires=3)

def circuit2():
    # 用于导出 a2 的电路    
    cir = dq.QubitCircuit(4)
    # 初始化 x = [0,0,1]
    cir.x(2)

    # 应用我们的 oracle
    Uf(cir)

    # 我们测量最后一个量子比特
    cir()
    return cir.measure(wires=3)

# 我们为 x = [1,0,0] 运行
a0 = circuit0()

# 我们为 x = [0,1,0] 运行
a1 = circuit1()

# 我们为 x = [0,0,1] 运行
a2 = circuit2()

print(f"'a' 的值为 [{a0},{a1},{a2}]")

'a' 的值为 [{'0': 1024},{'1': 1024},{'1': 1024}]

在这种情况下，通过 3 次查询（ n=3 ），我们已经发现了 \vec{a} 的值。让我们运行 Bernstein-Vazirani 子程序（这次将量子比特真正用作量子比特）来验证一次调用就足够了：

def circuit():
    cir = dq.QubitCircuit(4)
    # 我们初始化为 |0001>
    cir.x(3)

    # 执行哈达玛门操作
    cir.hlayer()

    # 应用我们的函数
    Uf(cir)

    # 再次执行哈达玛门操作
    for i in range(3):
        cir.h(wires=i)

    # 测量前三个量子比特
    cir()
    return cir.measure(wires=[0,1,2])

a = circuit()

print(f"a 的值是 {a}")

a 的值是 {'011': 1024}

一切都如预期的那样工作，我们已经成功执行了 Bernstein-Vazirani 算法。需要注意的是，由于我们设备的定义方式，我们只使用一次测量就找到了这个值。

参考文献

[1] Bernstein E, Vazirani U. Quantum complexity theory[C]//Proceedings of the twenty-fifth annual ACM symposium on Theory of computing. 1993: 11-20.

文档链接

案例代码