![]()
Hadamard Test
量子Hadamard测试是一个用来估计量子态和量子操作的特定属性的量子算法。它可以用来测量一个量子态的相位,或者更一般地,用来测量量子态和量子门操作之间的重叠。
下面将详细解释Hadamard测试的基本步骤。这里我们考虑最简单的形式,即用来测量一个酉操作(量子门)U对应于特定量子态|\psi\rangle的效果。
Hadamard Test的设置
我们需要两个寄存器:
- 控制寄存器:一个量子比特,初始状态为|0\rangle。
- 目标寄存器:可以是单个量子比特或者多个量子比特,其初始状态为|\psi\rangle。
Hadamard Test的步骤
- 初始化:
首先,我们将控制寄存器的量子比特准备在|0\rangle状态,目标寄存器的量子比特准备在|\psi\rangle状态。 -
应用Hadamard门:
然后,我们对控制寄存器的量子比特应用一个Hadamard门H。Hadamard门会将|0\rangle和|1\rangle态变换到叠加态\frac{|0\rangle + |1\rangle}{\sqrt{2}}和\frac{|0\rangle – |1\rangle}{\sqrt{2}}。经过这一步骤后,控制寄存器的状态变为:
\frac{|0\rangle + |1\rangle}{\sqrt{2}} -
控制操作:
接下来,我们执行一个控制U操作。这意味着如果控制寄存器在|1\rangle状态,那么U将会作用在目标寄存器的量子比特上。如果控制寄存器在|0\rangle状态,则目标寄存器的状态不变。操作后的整体状态变为:
\frac{|0\rangle \otimes |\psi\rangle + |1\rangle \otimes U|\psi\rangle}{\sqrt{2}} -
再次应用Hadamard门:
接着,我们在控制寄存器上再次应用Hadamard门。这会将控制寄存器的|0\rangle和|1\rangle分量与目标寄存器的状态进行进一步的叠加。这时候的整体状态将是:
- 测量控制寄存器:
最后,我们测量控制寄存器。测量结果将会是|0\rangle或者|1\rangle。测量结果的概率分布取决于|\psi\rangle和U|\psi\rangle的重叠程度。
测量结果和|\psi\rangle与U|\psi\rangle的关系是:
- 测量控制寄存器得到|0\rangle的概率是P(0) = \frac{1 + \mathrm{Re}\langle\psi|U|\psi\rangle}{2}。
- 测量控制寄存器得到|1\rangle的概率是P(1) = \frac{1 – \mathrm{Re}\langle\psi|U|\psi\rangle}{2}。
通过这些概率,我们可以估计量子Hadamard测试是一种量子算法,它可以用来估计和测量量子态的某些特性,比如和一个酉操作(量子门)的相位关系。这种测试的基本思想是利用量子叠加和干涉的性质来提取信息。
代码实例
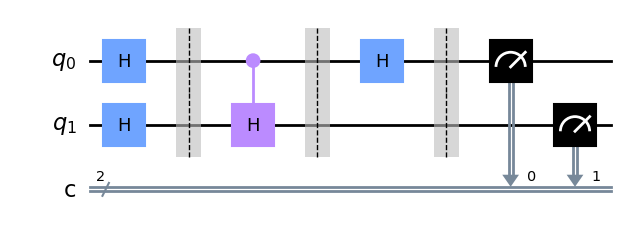
取 \left|\psi\right\rangle=\frac{\left|0\right\rangle+\left|1\right\rangle}{\sqrt2},U=H,Hadamard Test的一个DeepQuantum代码实例如下:
import deepquantum as dq
import numpy as np
def Hadamard_Test():
cir = dq.QubitCircuit(2)
# 应用Hadamard门
cir.h(0)
cir.h(1)
cir.barrier()
# 控制操作
cir.h(1,0)
cir.barrier()
# 再次应用Hadamard门
cir.h(0)
cir.barrier()
# 测量控制寄存器
cir.measure(0)
return cir
# 绘制量子线路图
Hadamard_Test_circuit = Hadamard_Test()
Hadamard_Test_circuit.draw()
输出结果应如下所示,分别以 \frac{1+\sqrt2/2}{2} 和 1-\frac{1+\sqrt2/2}{2} 的概率得到 |0⟩和 |1⟩ :
res = Hadamard_Test_circuit.measure(shots=10000)
p_0=(res['00']+res['01'])/(res['00']+res['01']+res['10']+res['11'])
p_1=(res['10']+res['11'])/(res['00']+res['01']+res['10']+res['11'])
print("p_0:"+str(p_0))
print("p_1:"+str(p_1))
p_0:0.8536
p_1:0.1464


