氢分子基态能量求解的基础理论

波恩-奥本海默近似

原子单位制中 $H_2$ 分子的哈密顿量如下图所示:

$\mathcal{H}=-\frac{1}{2} \sum_{i} \nabla_{i}^{2}-\frac{1}{2} \sum_{A} \frac{\nabla_{A}^{2}}{M_{A}}-\sum_{i}\sum_{A} \frac{Z_{A}}{r_{iA}}+\sum_{i}\sum_{j>i} \frac{1}{r_{ij}}+\sum_{A}\sum_{B>A} \frac{Z_{A}Z_{B}}{R_{AB}}$

在原子单位制中，单位电荷 $e$ 被归一化为1，电子质量 $m_e$ 被归一化为1，真空电容率 $4\pi\epsilon_0$ 被归一化为1，同时所有的长度单位都以玻尔半径 $a_0$ 为单位， $a_0 \approx 5.29177 \times 10^{-11}m$ 。

上式中 $i,j$ 表示电子指标， $A, B$ 表示原子核指标， $M_A$ 和 $Z_A$ 表示原子核 $A$ 的原子序数和质量。 $r_{ij}$ 表示电子之间的距离， $R_{AB}$ 表示原子核之间的距离。上式中从左到右每一项分别对应着电子的动能项，原子核的动能项，电子和原子核之间的库伦引力，电子之间的库伦斥力，原子核之间的库伦斥力。

在波恩-奥本海默近似中，假设电子在固定不动的原子核产生的电场中运动，那么原子核的动能项可以忽略，原子核的势能项是一个常数， $H_2$ 分子的哈密顿量可以简化为:

$\mathcal{H}_{\mathrm{elec}}=-\frac12\sum_i \nabla_i^2-\sum_i\sum_A \frac{Z_A}{r_{iA}}+\sum_i\sum_{j>i} \frac1{r_{ij}}$

求解 $H_2$ 分子的基态能量问题就变成了求解下面薛定谔方程的本征值问题:

$\mathcal{H}_{\mathrm{elec}}\Psi_\mu(r) = E_\mu\Psi_\mu(r)$

$\Psi_\mu(r)$ 是电子波函数，对应着本征能量 $E_\mu$ 。

Hartree-Fock 方法

Slater 行列式

Hartree-Fock 方法引入一组单电子轨道来构造多电子体系波函数，从而将多体问题简化为单体问题。对于二电子体系，引入两个空间轨道 $\phi_1(r_1)、\phi_2(r_2)$ 来表示电子的波函数。一般的有

$\Psi(r_1, r_2) = \phi_1(r_1)\phi_2(r_2)$

但是对于费米子体系而言需要满足交换反对称性，因此电子波函数表示应该写成

$\Psi(r_1, r_2) = \frac{1}{\sqrt{2}}(\phi_1(r_1)\phi_2(r_2)- \phi_2(r_1)\phi_1(r_2))$

可以引入Slater 行列式来表示

$\Psi(r_1, r_2) = \frac{1}{\sqrt{2}} \left|\begin{array}{cc} \phi_1(r_1) & \phi_2(r_1)\\\\ \phi_1(r_2) & \phi_2(r_2) \end{array} \right|$

但是考虑更一般的情况，将电子的自旋(spin)考虑进去，对应的两个空间轨道波函数扩展为四个自旋轨道波函数，它们的对应如下：
$\chi_0(x) = \phi_1(r)\alpha(\omega)$
$\chi_1(x) = \phi_1(r)\beta(\omega)$
$\chi_2(x) = \phi_2(r)\alpha(\omega)$
$\chi_3(x) = \phi_2(r)\beta(\omega) \\$
$\chi_0(x), \chi_1(x), \chi_2(x), \chi_3(x)$ 对应四个自旋轨道波函数, $\alpha(\omega), \beta(\omega)$ 分别对应自旋向上波函数和自旋向下波函数。那么更一般的情况下Slater 行列式如下

$\Psi(x_1,…, x_N) = \frac{1}{\sqrt{N!}} \left|\begin{array}{ccc} \chi_1(x_1) & …& \chi_N(x_1)\\\\ … & …& …\\\\ \chi_1(x_N) & …& \chi_N(x_N)\\\\ \end{array} \right|$

二次量子化

$H_2$ 分子的两个电子对应四个自旋轨道波函数 $\chi_0(x), \chi_1(x), \chi_2(x), \chi_3(x)$ 共有6种组合方式，那么对应的基矢量有6个。我们采用类似玻色系统中的Fock态表示，但是对应的物理含义不同，比如量子态 $|0,1 \rangle_F$ 表示两个电子分别占据了前两个轨道。 $H_2$ 分子的双电子波函数可以表示为

类似玻色系统中的处理，这里可以引入对应的生成算符 $f^\dagger_p$ 和湮灭算符 $f_p$ , 他们满足下面的代数关系：

$\{f^\dagger_p, f^\dagger_q\} = f^\dagger_pf^\dagger_q + f^\dagger_qf^\dagger_p = 0 \\\\ \{f_p, f^\dagger_q\} = f_pf^\dagger_q + f^\dagger_qf_p = \delta_{pq}$

对应的量子态可以通过生成算符作用到真空态 $|-\rangle_F$ 表示

二电子体系的哈密顿可以用生成算符和湮灭算符表示[1]:

$H_{\mathrm{elec}}=\sum_{pq}h_q^p f_p^\dagger f_q+\frac12 \sum_{pqrs}v_{rs}^{pq} f_p^\dagger f_q^\dagger f_rf_s$

$p, q, r, s$ 表示自旋轨道， $h^p_q, v^{pq}_{rs}$ 对应单电子积分和双电子积分，它们的数值可以通过计算化学库 openfermion 得到。

$h_{q}^{p}=\int d\mathbf{x} \chi_{p}^{*}(\mathbf{x}) \Big(-\frac{1}{2}\nabla^{2}-\sum_{A} \frac{Z_{A}}{r_{A}}\Big) \chi_{q}(\mathbf{x}),$

$v_{rs}^{pq}=\int d\mathbf{x}_1 d\mathbf{x}_2 \frac{\chi_p^*(\mathbf{x}_1)\chi_q^*(\mathbf{x}_2) \chi_r(\mathbf{x}_2)\chi_s(\mathbf{x}_1)}{r_{12}},$

Hartree-Fock方法只考虑哈密顿量中电子非相互作用的部分,

$H_{F}=\sum_{pq}h_{q}^{p} f_{p}^{\dagger}f_{q}$

因此得到的基态能量比真实的基态能量要高。

费米子体系到玻色子体系的映射

费米子量子态到玻色子量子态的映射

文献[1] 中详细介绍了如何将量子态从费米子系统映射到玻色子系统。首先对与玻色子系统的湮灭算符 $b$ 和生成算符 $b^\dagger$ 满足下面的对易关系

$[b_p^\dagger,b_q^\dagger]=b_p^\dagger b_q^\dagger-b_q^\dagger b_p^\dagger=0 \\\\ [b_p,b_q^\dagger]=b_pb_q^\dagger-b_q^\dagger b_p=\delta_{pq}$

对应的Fock态表示如下:

$|q_1,\cdots,q_N\rangle_B\equiv\frac{(b_1^\dagger)^{q_1}\cdots(b_N^\dagger)^{q_N}}{\sqrt{q_1!\cdots q_N!}}\left|0,\cdots,0\right\rangle_B$

文献[1] 给出了一个单射实现量子态从费米子系统到玻色子系统的映射

$\left|p_1,\cdots,p_N\right\rangle_F\leftrightarrow\left|q_1,\cdots,q_N\right\rangle_B$

具体的映射规则如下：

$q_j = \begin{cases} p_1, if j=N \\\\ p_{N-j+1} – p_{N-j} – 1, if j\neq N \end{cases}$

对于 $H_2$ 分子的四个自旋轨道的6个基矢，对应到玻色系统的Fock态如下：

$|0,1\rangle_{F}\leftrightarrow|0,0\rangle_{B} ,\quad|0,2\rangle_{F}\leftrightarrow|1,0\rangle_{B} ,\quad|0,3\rangle_{F}\leftrightarrow|2,0\rangle_{B} ,\\|1,2\rangle_{F}\leftrightarrow|0,1\rangle_{B} ,\quad|1,3\rangle_{F}\leftrightarrow|1,1\rangle_{B} ,\quad|2,3\rangle_{F}\leftrightarrow|0,2\rangle_{B}$

对于费米子系统能量最低的基矢是两个电子分别占据最低的两个轨道，对应着量子态 $|0, 1\rangle_F$ ，映射到玻色系统中对应着真空态 $|0, 0\rangle_B$ 。

费米子算符到玻色子算符的映射

在费米子系统中可以类比粒子数算符引入一个费米算符 $E^p_q$ ,
$E^p_q = f^\dagger_p f_q = (E^q_p)^\dagger$
当 $p=q$ 时， $E^p_p$ 等价于粒子数算符， $p\neq q$ 时 $E^p_q$ 可以理解为激发算符。

二次量子化后的哈密顿量可以用算符 $E^p_q$ 表示，

$\begin{aligned} H_{\mathrm{elec}}& =\Big[\frac{1}{2} \sum_{p}h_{p}^{p} E_{p}^{p}+\sum_{p>q}\Big(h_{q}^{p} E_{q}^{p}+\frac{1}{2} \tau_{qp}^{pq} E_{p}^{p}E_{q}^{q}\Big) \\\\ &+\sum_{p>q>r}\left(\tau_{rp}^{pq} E_p^pE_r^q+\tau_{qr}^{pq} E_q^qE_r^p+\tau_{rq}^{pr} E_r^rE_q^p\right) \\\\ &+\sum_{p>q>r>s}\left(\tau_{sr}^{pq} E_{r}^{p}E_{s}^{q}+\tau_{sq}^{pr} E_{q}^{p}E_{s}^{r}+\tau_{rq}^{ps} E_{q}^{p}(E_{s}^{r})^{\dagger}\right)\Big]+\mathrm{h.c.}, \end{aligned}$

下面考虑将费米算符 $E^p_q$ 映射到玻色系统，来完成哈密顿量的映射。

2.1 首先考虑单电子的情况 $(N=1)$ ，对应的量子态映射如下
$|j\rangle_F \leftrightarrow |j\rangle_B$
$E_{p}^{p}$ 作用到 $|j\rangle_F$ 结果如下

$E_{p}^{p}|j\rangle_{\mathrm{F}}=f_{p}^{+}f_{p}|j\rangle_{\mathrm{F}}=\delta_{pj}|j\rangle_{F}$

映射到玻色子体系中 $O_B$ 的作用如下
$O_B |j\rangle_B = \delta_{pj} |j\rangle_B$
可以得到 $O_B = |p\rangle_B \langle p|_B$ , 那么有下面的映射关系
$E_p^p \leftrightarrow |p\rangle_B \langle p|_B$
$E_{q+p}^{p}$ 作用到 $|j\rangle_F$ 结果如下:

$\begin{aligned}E_{q}^{q+p}|j\rangle_{\mathrm{F}} &=f_{q+p}^{+}f_{q}f_{j}^{+}|-\rangle_{\mathrm{F}}\\\\ &=\delta_{qj}f_{q+p}^{+}|-\rangle_{F}\\\\ &=\delta_{qj}|j+p\rangle_{F}\end{aligned}$

对应到玻色系统的映射如下：

$E_{q+p}^p \leftrightarrow (\sigma^\dagger)^p|q\rangle_B \langle q|_B$

$\sigma^\dagger$ 是归一化玻色子生成算符。

2.2 考虑二电子的情况 $(N=2)$

$E_r^r\left|p,q\right\rangle_F=\left(\delta_{p,r}+\delta_{q,r}\right)\left|p,q\right\rangle_F$

$E_p^p\leftrightarrow{I}\otimes|p\rangle \langle p|+\sum_{a+b=p-1}|a,b\rangle \langle a,b|$

$\begin{aligned} E_q^{q+p}& \leftrightarrow\sigma_{1}^{p} (\sigma_{2}^{\dagger})^{p} \sum_{a=0}^{\infty} |p+a,q\rangle \langle p+a,q|-\sum_{a=0}^{p-2} (\sigma_{1}^{\dagger})^{p-2-a} \sigma_{1}^{a} (\sigma_{2}^{\dagger})^{a+1} |a,q\rangle \langle a,q| \\\\ &+(\sigma_1^\dagger)^p\sum_{a+b=q-1}|a,b\rangle \langle a,b| . \end{aligned}$

下面是几个简单的例子：

$\begin{aligned} &E_0^0 \leftrightarrow{I}\otimes|0\rangle\left\langle0\right|, \\\\ &E_1^1\leftrightarrow{I}\otimes\left|1\right\rangle\left\langle1\right|+\left|0,0\right\rangle\left\langle0,0\right| \\\\ &E_0^1 \leftrightarrow\sum_{j=1}^{L} |j-1,1\rangle \langle j,0| , \\\\ &\text{E}_0 ^{2}\leftrightarrow\Big(\sum^{L-1}|j-1,2\rangle \langle j+1,0| \Big)-|0,1\rangle \langle0,0| , \end{aligned}$

因为这里只涉及到二电子体系，对于更大的体系可以参考文献[1]，这里不再讨论。

得到上述的映射关系之后，只需要将二次量子化后的二电子哈密顿量映射到玻色子体系中，就可以将求解费米子体系基态问题过渡到玻色子体系的基态问题。

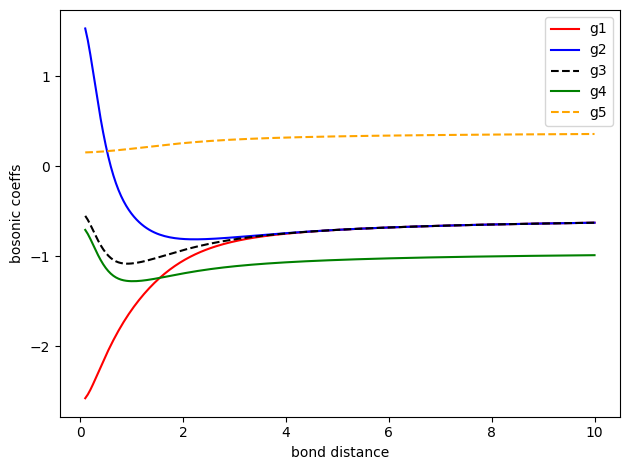
$\begin{aligned}H_{F}&=(h_{0}^{0}+v_{10}^{01}+v_{30}^{03}+v_{20}^{02}-v_{02}^{02}) E_{0}^{0}+(h_{1}^{1}+v_{21}^{12}+v_{31}^{13}-v_{13}^{13}) E_{1}^{1}+(h_{2}^{2}+v_{32}^{23}) E_{2}^{2}+h_{3}^{3} E_{3}^{3}-v_{10}^{01} E_{1}^{0}E_{0}^{1}-v_{32}^{23} E_{2}^{2}E_{2}^{3}-v_{30}^{03} E_{3}^{0}E_{0}^{3}-v_{21}^{12} E_{2}^{1}E_{1}^{2}-(v_{20}^{02}-v_{02}^{02}) E_{2}^{0}E_{0}^{2}-(v_{31}^{13}-v_{13}^{13}) E_{3}^{1}E_{1}^{3}-v_{12}^{03} (E_{1}^{0}E_{2}^{3}+\mathrm{h.c.})-v_{32}^{01} (E_{3}^{0}E_{2}^{1}+\mathrm{h.c.})\end{aligned}$

$\begin{aligned} H_{F}\leftrightarrow H_{B}& =g_{1}\left|0,0\right\rangle\left\langle0,0\right|+g_{2}\left|0,2\right\rangle\left\langle0,2\right|+g_{3}\left(\left|0,1\right\rangle\left\langle0,1\right|+\left|2,0\right\rangle\left\langle2,0\right|\right) \\\\ &+g_4\big( |1,0\rangle \langle1,0|+|1,1\rangle \langle1,1| \big)+g_5 \big( |0,0\rangle \langle0,2|+\mathrm{h.c.}\big) \\\\ &- g_{5} ( |2,0\rangle \langle0,1|+\mathrm{h.c.}), \end{aligned}$

$g_1, g_2, g_3, g_4, g_5$ 用单电子积分和双电子积分表示如下

$\begin{array}{ll}\hline\text{Coefficient}&\text{Definition}\\\\\hline g_1&h_0^0+h_1^1+v_{10}^{01}\\\\g_2&2h_2^2+v_{32}^{23}\\\\g_3&h_0^0+h_2^2+v_{20}^{02}\\\\g_4&h_0^0+h_2^2+v_{20}^{02}-v_{02}^{02}\\\\g_5&v_{02}^{02}\\\\\hline\end{array}$

对应的数值随原子核距离变化如下

import deepquantum as dq
import matplotlib.pyplot as plt
import numpy as np
import torch
from scipy import io

dic = io.loadmat('boson_coeff2.mat')
g1 = dic['g1'][0]
g2 = dic['g2'][0]
g3 = dic['g3'][0]
g4 = dic['g4'][0]
g5 = dic['g5'][0]

#######################
# %matplotlib notebook
fig = plt.figure()
# R_values = np.linspace(0.1, 3, 50)
R_values = np.linspace(0.1, 10, 50*4)
plt.plot(R_values, dic['g1'][0], label='g1', color='red')
plt.plot(R_values, dic['g2'][0], label='g2', color='blue')
plt.plot(R_values, dic['g3'][0], label='g3', color='black', ls='--')
plt.plot(R_values, dic['g4'][0], label='g4', color='green')
plt.plot(R_values, dic['g5'][0], label='g5', color='orange', ls='--')

plt.xlabel('bond distance')
plt.ylabel('bosonic coeffs')
plt.tight_layout()
plt.legend()

变分量子求解器(VQE)

变分量子求解器(VQE) 是一种混合量子-经典算法[2]，广泛应用于计算化学和物理中的量子态能量问题。VQE利用量子计算机处理量子态的叠加和纠缠，通过变分原理逼近系统的基态能量，其中基态能量通过在量子计算机上测量得到，变分过程在经典计算机上完成。量子测量得到的基态能量和真实的能量关系如下：

$E_\mathrm{vqe} = \frac{\langle \Phi_t |H|\Phi_t \rangle}{\langle \Phi_t |\Phi_t \rangle}\geq E_\mathrm{real}$

$|\Phi_t \rangle$ 表示试探波函数。

在变分过程中，使用参数化波函数 $|\Phi_t (\theta) \rangle$ ，不断迭代变分参数 $\theta$ 使得 $|\Phi_t (\theta) \rangle$ 接近真实的波函数，从而得到更准确的基态能量值。

VQE的一般步骤如下：
1. 构造哈密顿量，将量子化学问题对应的哈密顿量映射成可变分的量子线路。
2. 选择参数化量子态和量子线路，得到一个参数化量子态 $|\Phi_t (\theta) \rangle$ ，参数 $\theta$ 可以对应到量子门或者光量子门的参数等。
3. 算符基矢的期望值测量，对于各个算符基矢测量并计算对应的平均值。
4. 哈密顿量的期望值测量，通过各个算符基矢的测量值计算当前波函数下的哈密顿量平均值 $E(\theta)$ 。
5. 经典变分算法迭代优化哈密顿量平均值：通过梯度下降等算法更新参数 $\theta$ ，得到能量更低的 $E(\theta)$ 。

变分量子算法的光量子线路实现

根据前面的讨论可以知道，考虑四个自旋轨道的二电子体系波函数映射到玻色系统中对应的波函数表示如下：

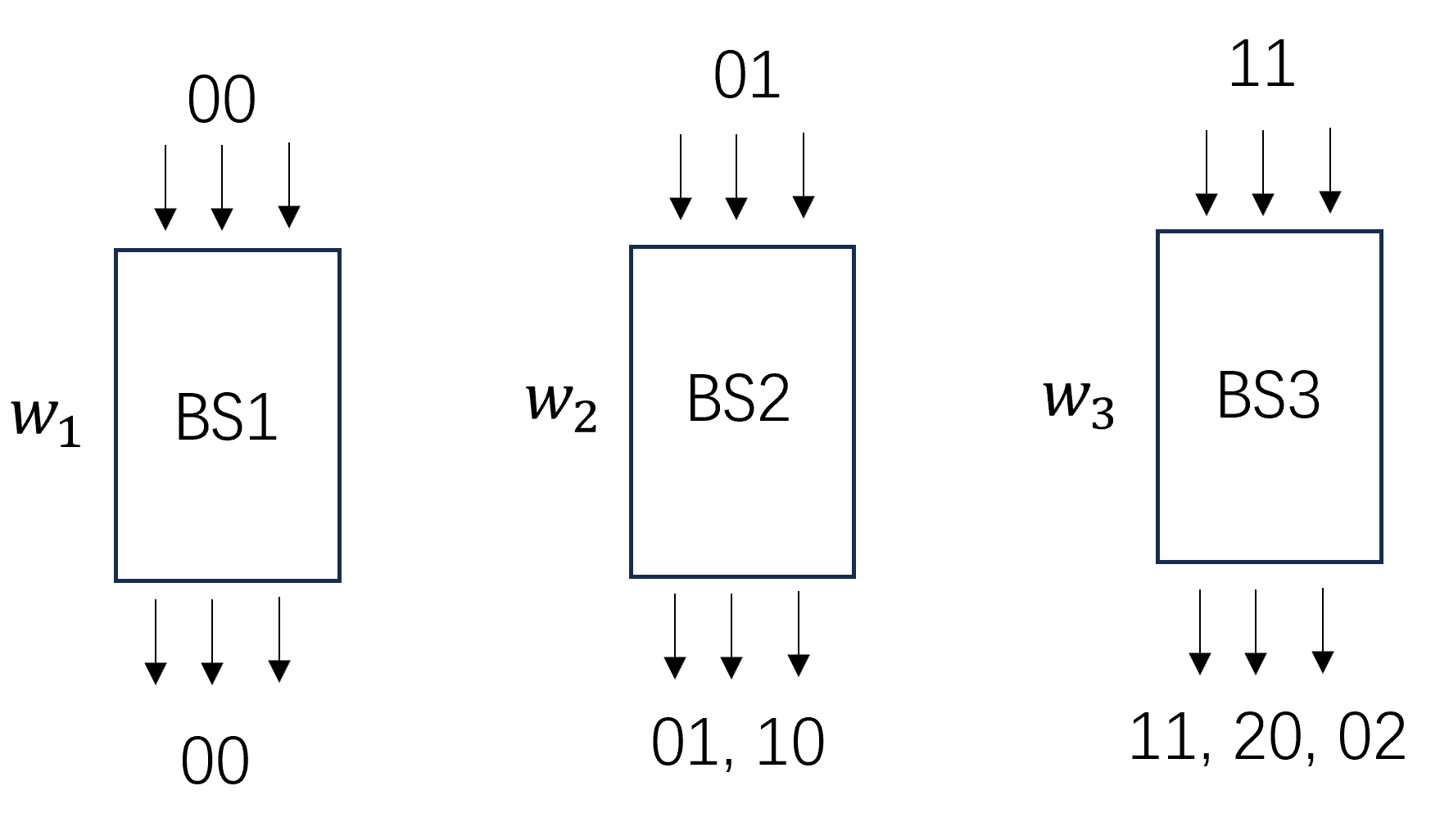
3个玻色采样线路输出分别对应上面的3组基矢，同时为了归一化给每个玻色采样线路加入权重 $w_1, w_2, w_3$ 。
$w_1^2 + w_2^2 + w_3^2 = 1$
最后将输出的量子态组合为:

可以验证对应的振幅是归一化的。

玻色采样线路的实现

对于单个玻色采样线路，只需要下图的两模光量子线路即可，

三个线路的结构是相同的，不同之处在于更换不同的输入只需要更新不同的线路参数即可，同时对于输入为 $|0,0 \rangle_B$ 的线路，只有一个确定的结果输出(不考虑损耗)，不需要进行变分，因此只需要通过变分优化两个玻色采样线路参数以及3个权重即可。

代码实现

两模玻色采样线路的VQE实现

def exp_h(paras):
    w1, w2, w3 = torch.nn.functional.normalize(abs(paras[0:3]), dim=0) # 归一化
    amp_00 = w1
    ############################
    nmode = 2
    cir2 = dq.QumodeCircuit(nmode=nmode, init_state=[0,1], cutoff=3, backend='fock', basis=True)
    cir2.ps(0, inputs=paras[3] )
    cir2.ps(1, inputs=paras[4])
    cir2.bs([0,1], inputs=[paras[5], paras[6]])
    cir2.ps(0, inputs=paras[7])
    cir2.ps(1, inputs=[8])
    state2 = cir2(is_prob=False)
    amp_01 = w2 * state2[state_01]
    amp_10 = w2 * state2[state_10]
    ############################
    cir3 = dq.QumodeCircuit(nmode=nmode, init_state=[1,1], cutoff=3, backend='fock', basis=True)
    cir3.ps(0, inputs=paras[9] )
    cir3.ps(1, inputs=paras[10])
    cir3.bs([0,1], inputs=[paras[11], paras[12]])
    cir3.ps(0, inputs=paras[13])
    cir3.ps(1, inputs=[14])
    state3 = cir3(is_prob=False)
    amp_11 = w3 * state3[state_11]
    amp_20 = w3 * state3[state_20]
    amp_02 = w3 * state3[state_02]
    exp_h  = g_1*abs(amp_00)**2 + g_2*abs(amp_02)**2 + g_3*(abs(amp_01)**2+abs(amp_20)**2) + \
             g_4 *(abs(amp_10)**2 + abs(amp_11)**2) + g_5*(amp_00.conj()*amp_02+amp_00*amp_02.conj()) - \
             g_5* (amp_20.conj()*amp_01+amp_20*amp_01.conj()) # see

    return (exp_h).real

state_01 = dq.FockState([0,1])
state_10 = dq.FockState([1,0])
state_11 = dq.FockState([1,1])
state_20 = dq.FockState([2,0])
state_02 = dq.FockState([0,2])

energy_bs = [ ]
for idx in range(50):
    g_1 = g1[idx]
    g_2 = g2[idx]
    g_3 = g3[idx]
    g_4 = g4[idx]
    g_5 = g5[idx]

    w123 = torch.tensor([0.5, 0.5, 0.4], requires_grad=True)
    angles = torch.nn.Parameter(torch.randn(12))
    paras = torch.cat([w123, angles])
    optimizer =  torch.optim.Adam([w123, angles], lr=0.1)

    for epoch in range(150):
        optimizer.zero_grad()
        paras = torch.cat([w123, angles])
        loss = exp_h(paras)
        loss.backward() # backpropagetion
        optimizer.step() # update parameters
    energy_bs.append(loss)
    print(idx,loss,end='\r')

KeyboardInterrupt

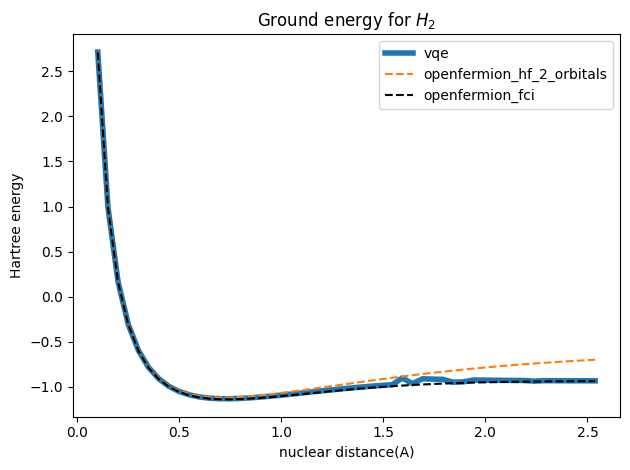
基态能量随原子核距离的变化

这里采用Hartree能量表示基态能量，一个Hartree能量等价于为 $27.2ev$ ，纵坐标表示Hartree能量, 横坐标为原子核的距离，对应的的单位为埃( $10^{-10}m$ )。

对比数据为考虑两个空间轨道的近似能量的HF方法，以及完全活性空间配置相互作用(Full Configuration Interaction，FCI)，FCI方法是量子化学中最精确的电子结构计算方法之一。它通过在给定基组内考虑所有可能的电子配置（即所有可能的电子占据状态），以尽可能准确地描述多电子系统的波函数，尽管FCI因为计算成本太高而无法应用于大多数实际化学系统，但它在小体系中被用作“金标准”来验证其他近似方法（如CC、MP2、DFT）的准确性。

R_values = R_values[0:50]
hartree_dis = R_values/0.529177 # using Bohr radius
openfermion_h2 = np.load('openfermion_h2_v3.npy')
openfermion_h2_fci = np.load('openfermion_h2_fci.npy')
# %matplotlib notebook
fig =  plt.figure()
nuclear_v = 1/hartree_dis
plt.plot(R_values, torch.stack(energy_bs).mT[0].detach().numpy() + nuclear_v,lw=4, label='vqe')
plt.plot(R_values, openfermion_h2[0:50], ls='--', label='openfermion_hf_2_orbitals')
plt.plot(R_values, openfermion_h2_fci[0:50], ls='--', label='openfermion_fci', color='black')
plt.ylabel('Hartree energy')
plt.xlabel('nuclear distance(A)')
plt.title('Ground energy for  $H_2$ ')
plt.legend()
plt.tight_layout()

两模高斯玻色采样线路的VQE实现

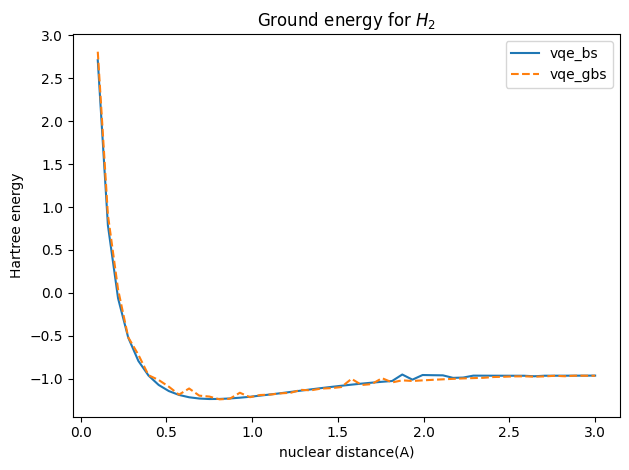
同时我们也可以用高斯玻色采样做VQE变分求解 $H_2$ 的基态能量，但是不同之处在于高斯玻色采样线路输出的高斯态对应的Fock基矢叠加一般是无穷多项，因此需要在我们需要的希尔伯特空间做截断然后归一化，这一步相当于实验上的后选择操作。与此同时带来的好处是只需要一张光量子芯片结合压缩光源就可以完成变分任务。下面演示通过加入压缩门和位移门来构造高斯玻色采样线路进行变分。

nmode = 2
cir = dq.QumodeCircuit(nmode=nmode, init_state='vac', cutoff=3, backend='fock', basis=False)
cir.s(0, r=1)
cir.s(1, r=1)
cir.d(0, r=1)
cir.d(1, r=1)
cir.ps(0)
cir.ps(1)
cir.bs([0,1])
cir.d(0)
cir.d(1)
cir.draw()
# state = cir()

def exp_h_gbs_fock(paras):
    s1, s2 = torch.nn.functional.normalize(abs(paras[0:2]), dim=0) # 归一化
    nmode = 2
    cir = dq.QumodeCircuit(nmode=nmode, init_state='vac', cutoff=3, backend='fock', basis=False)
    cir.s(0, r=s1)
    cir.s(1, r=s2)
    cir.d(0, r=paras[2])
    cir.d(1, r=paras[3])
    cir.ps(0, paras[4])
    cir.ps(1, paras[5])
    cir.bs([0,1], inputs=[paras[6], paras[7]])
    cir.d(0, r=paras[8])
    cir.d(1, r=paras[9])
    # cir.to(torch.double)
    state = cir()
    p_00 = state[0][0,0]
    p_01 = state[0][0,1]
    p_10 = state[0][1,0]
    p_11 = state[0][1,1]
    p_20 = state[0][2,0]
    p_02 = state[0][0,2]
    p_list = torch.stack([p_00, p_01, p_10, p_11, p_20, p_02])
    p_00_,p_01_,p_10_,p_11_,p_20_,p_02_ = torch.nn.functional.normalize(p_list, dim=0)

    exp_h  = g_1*abs(p_00_)**2 + g_2*abs(p_02_)**2 + g_3*(abs(p_01_)**2+ abs(p_20_)**2) + \
             g_4 *(abs(p_10_)**2 + abs(p_11_)**2) + g_5*(p_00_.conj()*p_02_+p_00_*p_02_.conj()) - \
             g_5* (p_20_.conj()*p_01_+p_20_*p_01_.conj()) # see

    return (exp_h).real

energy_gbs = [ ]
for idx in range(50):
    g_1 = g1[idx]
    g_2 = g2[idx]
    g_3 = g3[idx]
    g_4 = g4[idx]
    g_5 = g5[idx]

    angles = torch.nn.Parameter(torch.randn(10))
    optimizer =  torch.optim.Adam([angles], lr=0.1)
    for epoch in range(150):
        optimizer.zero_grad()
        loss = exp_h_gbs_fock(angles)
        loss.backward() # backpropagetion
        optimizer.step() # update parameters
    energy_gbs.append(loss)
    print(idx,loss,end='\r')

49 tensor(-1.1422, grad_fn=<SelectBackward0>)

下面可以看到通过高斯玻色采样线路的变分结果也是非常接近玻色采样线路的变分结果的。

R_values = np.linspace(0.1, 3, 50)
hartree_dis = R_values/0.529177 # using Bohr radius
openfermion_h2 = np.load('openfermion_h2_v3.npy')
openfermion_h2_fci = np.load('openfermion_h2_fci.npy')
# %matplotlib notebook
fig =  plt.figure()
nuclear_v = 1/hartree_dis
plt.plot(R_values, torch.stack(energy_bs).mT[0].detach().numpy() + nuclear_v,lw=1.5, label='vqe_bs')
plt.plot(R_values, torch.stack(energy_gbs).detach().numpy() + nuclear_v,lw=1.5,ls='--', label='vqe_gbs')
plt.ylabel('Hartree energy')
plt.xlabel('nuclear distance(A)')
plt.title('Ground energy for  $H_2$ ')
plt.legend()
plt.tight_layout()