![]()
Simon 算法
本文首先介绍Simon问题,以及解决该问题的经典和量子算法。然后,我们使用 DeepQuantum 实现量子算法,并在模拟器和设备上运行。
1. 简介
Simon算法最早在参考文献[1]中提出,是第一个在解决特定问题时表现出指数级加速的量子算法,相比于最好的经典算法。这启发了基于量子傅里叶变换的量子算法,这种变换被用于最著名的量子算法:Shor算法。
1.1 Simon问题
给定一个未知的黑盒函数 f,保证其为一对一(1:1)或二对一(2:1)函数,一对一和二对一函数具有以下性质:
- 一对一:对每个输入映射一个唯一的输出。一个接受4个输入的函数示例为:
- 二对一:对每个唯一输出映射两个输入。一个接受4个输入的函数示例为:
这种二对一映射根据一个隐藏的比特串 b 进行,其中:
\text{给定 } x_1, x_2: \quad f(x_1) = f(x_2)
\text{可保证: } x_1 \oplus x_2 = b
给定这个黑盒函数 f,我们能多快判断出 f 是一对一还是二对一函数?然后,如果 f 是二对一的,我们能多快确定 b?事实证明,两种情况都归结为找出 b 的问题,其中 b={000…} 的比特串代表一对一函数 f。\oplus为异或操作。
1.2 Simon算法
经典解法
从经典的角度,如果想要100%确定给定 f 的 b 是什么,我们必须检查最多 2^{n-1}+1 个输入,其中n是输入的比特数。这意味着检查一半以上所有可能的输入,直到找到两个相同输出的情况。与 Deutsch-Jozsa 问题类似,如果幸运的话,我们可以在前两次尝试中解决问题。但如果碰到一个一对一的 f,或者在二对一 f 上非常不走运,那么我们就会被困在全部 2^{n-1}+1 个输入上。
已知存在下界为 \Omega(2^{n/2}) 的算法[2],但一般而言,复杂度随着n呈指数增长。
量子解法
实现Simon算法的量子线路如下图所示。
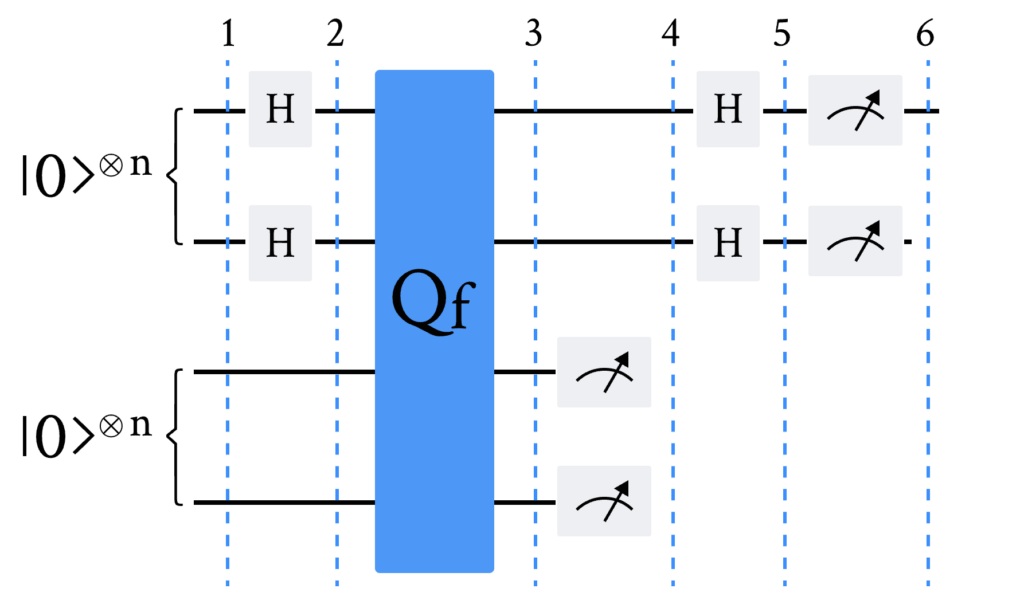
其中,查询函数 \text{Q}_f 作用于两个量子寄存器:
\lvert x \rangle \lvert a \rangle \rightarrow \lvert x \rangle \lvert a \oplus f(x) \rangle
特别地,当第二个寄存器处于态 |0\rangle = |00\dots0\rangle 时,有:
\lvert x \rangle \lvert 0 \rangle \rightarrow \lvert x \rangle \lvert f(x) \rangle
该算法包括以下步骤:
- 两个 n 比特输入寄存器初始化为零态: \lvert \psi_1 \rangle = \lvert 0 \rangle^{\otimes n} \lvert 0 \rangle^{\otimes n}
-
对第一个寄存器应用 Hadamard 变换: \lvert \psi_2 \rangle = \frac{1}{\sqrt{2^n}} \sum_{x \in {0,1}^{n} } \lvert x \rangle\lvert 0 \rangle^{\otimes n}
-
应用查询函数 \text{Q}_ f: \lvert \psi_3 \rangle = \frac{1}{\sqrt{2^n}} \sum_{x \in {0,1}^{n} } \lvert x \rangle \lvert f(x) \rangle
-
测量第二个寄存器。将观察到 f(x) 的某个值。由于问题的设置,观察到的值 f(x) 可能对应两个可能的输入:x 和 y = x \oplus b。因此第一个寄存器变为:
这里省略了第二个寄存器,因为它已被测量。
- 对第一个寄存器应用 Hadamard:
- 只有在以下条件下,测量第一个寄存器才会给出输出: (-1)^{x \cdot z} = (-1)^{y \cdot z} 这意味着: x \cdot z = y \cdot z\\ x \cdot z = \left( x \oplus b \right) \cdot z\\ x \cdot z = x \cdot z \oplus b \cdot z\\ b \cdot z = 0 \text{ (mod 2)} 将测量一个字符串 z,其与 b 的内积为0。因此,重复算法 \approx n 次,我们将能够获得 n 个不同的 z 值,并可以写出以下方程组: \begin{cases} b \cdot z_1 = 0\\b \cdot z_2 = 0\\\quad \vdots\\b \cdot z_n = 0 \end{cases} 先按位计算 b 和 z_n 的乘积,然后再将所有的乘积结果求和,最后看这个和是偶数还是奇数。由此可以确定 b,例如通过高斯消元法。
因此,在这个特定问题中,量子算法执行的步骤数比经典算法少指数级。
2. 示例
让我们来看一个 Simon 算法在 2 个量子比特上的示例,其中秘密字符串 b=11,使得当 y = x \oplus b 时,f(x) = f(y)。求解该问题的量子线路如下:
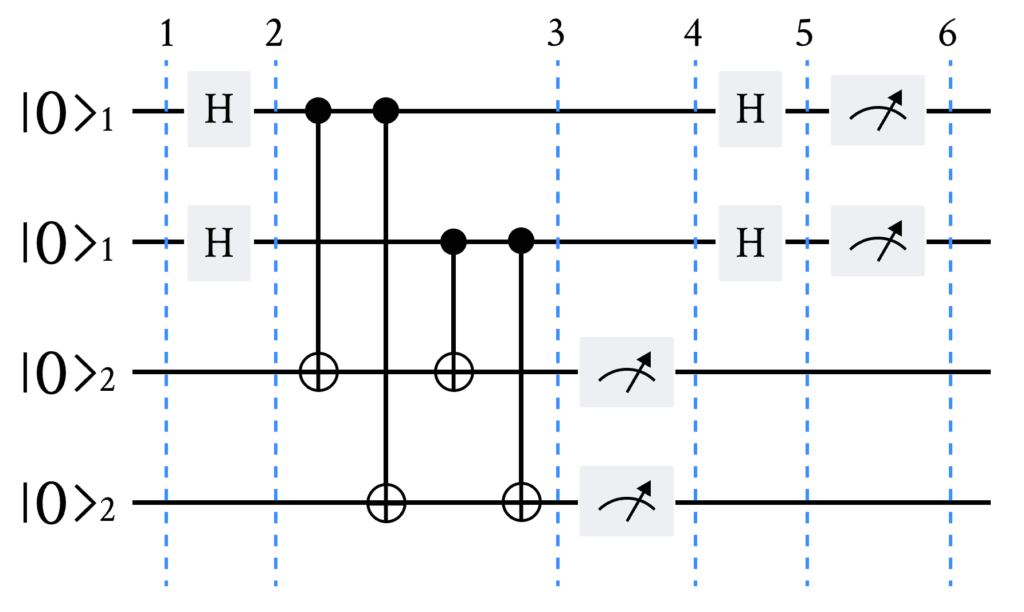
- 两个 2 量子比特输入寄存器被初始化为零态:
\lvert \psi_1 \rangle = \lvert 0 0 \rangle_1 \lvert 0 0 \rangle_2 -
对第一个寄存器中的量子比特应用 Hadamard 门:
- 对于字符串 b=11,查询函数可以实现为 \text{Q}_ f = CX_{1_a 2_a}CX_{1_a 2_b}CX_{1_b 2_a}CX_{1_b 2_b}(如上图线路图所示):
因此:
- 我们测量第二个寄存器。有 50\% 的概率会看到 \lvert 0 0 \rangle_2 或 \lvert 1 1 \rangle_2。为了示例的目的,让我们假设看到了 \lvert 1 1 \rangle_2。此时系统的状态为 \lvert \psi_4 \rangle = \frac{1}{\sqrt{2}} \left( \lvert 0 1 \rangle_1 + \lvert 1 0 \rangle_1 \right) 其中我们省略了第二个寄存器,因为它已经被测量过了。
-
对第一个寄存器应用 Hadamard 门
-
测量第一个寄存器会以相等的概率给出 \lvert 0 0 \rangle 或 \lvert 1 1 \rangle。
-
如果我们看到 \lvert 1 1 \rangle,则: b \cdot 11 = 0 这告诉我们 b \neq 01 或 10,剩下的两个可能的解是 b = 00 或 b = 11。请注意,b = 00 将始终是我们联立方程的一个平凡解。如果我们重复步骤 1-6 多次,我们只会测量到 |00\rangle 或 |11\rangle,因为 b \cdot 11 = 0 b \cdot 00 = 0 是满足 b=11 的唯一方程。我们可以通过选择一个随机输入(x_i)并检查 f(x_i) = f(x_i \oplus b) 来验证 b=11。例如: 01 \oplus b = 10 f(01) = f(10) = 11
3. DeepQuantum 实现
我们现在用 3 量子比特和 b=110 实现 Simon 算法。
import deepquantum as dq
import numpy as np
import matplotlib.pyplot as plt
函数 simon_oracle用于创建一个对应比特串 b 的 Simon 量子门。
在 DeepQuantum 中,测量操作只能在量子线路的末端进行。对于 Simon 算法来说,我们实际上不关心第二寄存器的输出,只会测量第一寄存器。
b = '110'
n = len(b)
def simon_oracle(b, n):
"""返回针对比特串b的Simon oracle"""
b = b[::-1] # 将b反转以便于迭代
cir = dq.QubitCircuit(n * 2)
# 执行复制;|x>|0> -> |x>|x>
for q in range(n):
cir.cx(q, q + n)
if '1' not in b:
return cir # 1:1映射,所以直接退出
i = b.find('1') # 在b中找到第一个非零比特的索引
# 如果q_i是1,则执行|x> -> |s.x>
for q in range(n):
if b[q] == '1':
cir.cx(i, q + n)
return cir
def simon_algorithm(b, n):
simon_circuit = dq.QubitCircuit(n * 2)
# 在查询oracle之前应用Hadamard门
for i in range(n):
simon_circuit.h(i)
simon_circuit.barrier()
# 应用oracle
simon_circuit += simon_oracle(b, n)
simon_circuit.barrier()
# 对输入寄存器应用Hadamard门
for i in range(n):
simon_circuit.h(i)
# 测量量子比特
simon_circuit.measure(wires=list(range(n)))
return simon_circuit
cir = simon_algorithm(b, n)
cir.draw()
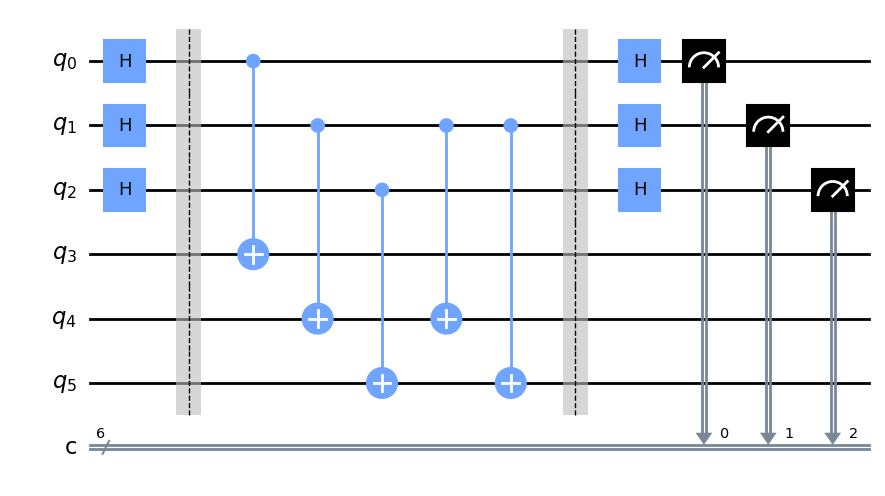
我们可以在模拟器上运行上述线路。
cir()
res = cir.measure(wires=list(range(n)))
res_reversed = {key[::-1]: value for key, value in res.items()}
print(res_reversed)
{'110': 271, '111': 245, '000': 238, '001': 270}
import matplotlib.pyplot as plt
# 键和值分别作为X轴和Y轴数据
keys = list(res_reversed.keys())
total = sum(res_reversed.values())
# 计算每个值相对于总和的比例
values = [value / total for value in res_reversed.values()]
# 创建柱状图
plt.bar(keys, values)
# 添加标题和轴标签
plt.xlabel('state')
plt.ylabel('Probabilities')
# 显示图形
plt.show()
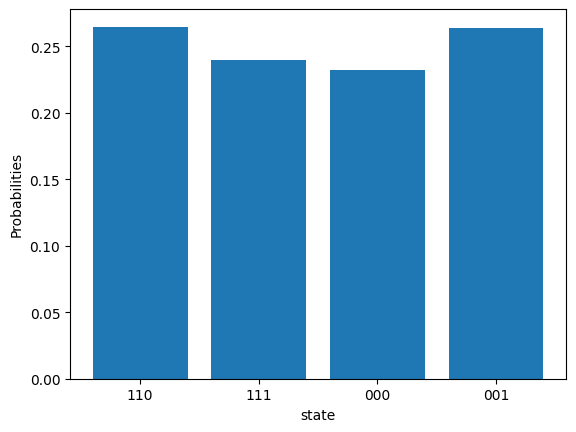
由于我们已经知道了 b,我们可以验证这些结果确实满足 b\cdot z = 0 \pmod{2}:
# 计算结果的点积
def bdotz(b, z):
return sum(int(b_i) * int(z_i) for b_i, z_i in zip(b, z)) % 2
# 假设res_reversed是一个包含结果的字典
# 遍历res_reversed的键,并打印b和z的点积(模2)
for z in res_reversed.keys():
print(f'{b}.{z} = {bdotz(b, z)} (mod 2)')
110.110 = 0 (mod 2)
110.111 = 0 (mod 2)
110.000 = 0 (mod 2)
110.001 = 0 (mod 2)
利用这些结果,我们可以通过解这组同时方程来找回 b = 110 的值。例如,假设我们首次测量得到 001,这告诉我们:
\begin{aligned}
b \cdot 001 &= 0 \\
(b_2 \cdot 0) + (b_1 \cdot 0) + (b_0 \cdot 1)&= 0 \\
(\cancel{b_2 \cdot 0}) + (\cancel{b_1 \cdot 0}) + (b_0 \cdot 1)&= 0 \\
b_0&= 0 \\
\end{aligned}
如果我们接下来测量 111,我们得到:
\begin{aligned}
b \cdot 111 &= 0 \\
(b_2 \cdot 1) + (b_1 \cdot 1) + (0 \cdot 1)&= 0 \\
(b_2 \cdot 1) + (b_1 \cdot 1) + (\cancel{0 \cdot 1})&= 0 \\
(b_2 \cdot 1) + (b_1 \cdot 1)&= 0 \\
\end{aligned}
这告诉我们可能是:
b_2 = b_1 = 0, \quad b = 000
或者
b_2 = b_1 = 1, \quad b = 110
其中 b = 110 是我们同时方程的非平凡解。我们可以使用高斯消元法来解决这些问题,其运行时间为 O(n^3)。
4. 参考文献
[1] Simon D R. On the power of quantum computation[J]. SIAM journal on computing, 1997, 26(5): 1474-1483.
[2] Cai G, Qiu D. Optimal separation in exact query complexities for Simon’s problem[J]. Journal of computer and system sciences, 2018, 97: 83-93.


