![]()
量子计数
为了理解这个算法,你首先需要理解 Grover 算法和量子相位估计算法。与 Grover 算法试图找到 Oracle 的解不同,量子计数算法告诉我们有多少这样的解。这个算法很有趣,因为它结合了量子搜索和量子相位估计。
1. 概述
1.1 直观理解
在量子计数中,我们只需使用量子相位估计算法来找到一个 Grover 搜索迭代的特征值。 Grover 算法的一次迭代 G 在 |\omega\rangle, |s’\rangle 基下将状态向量旋转 \theta:
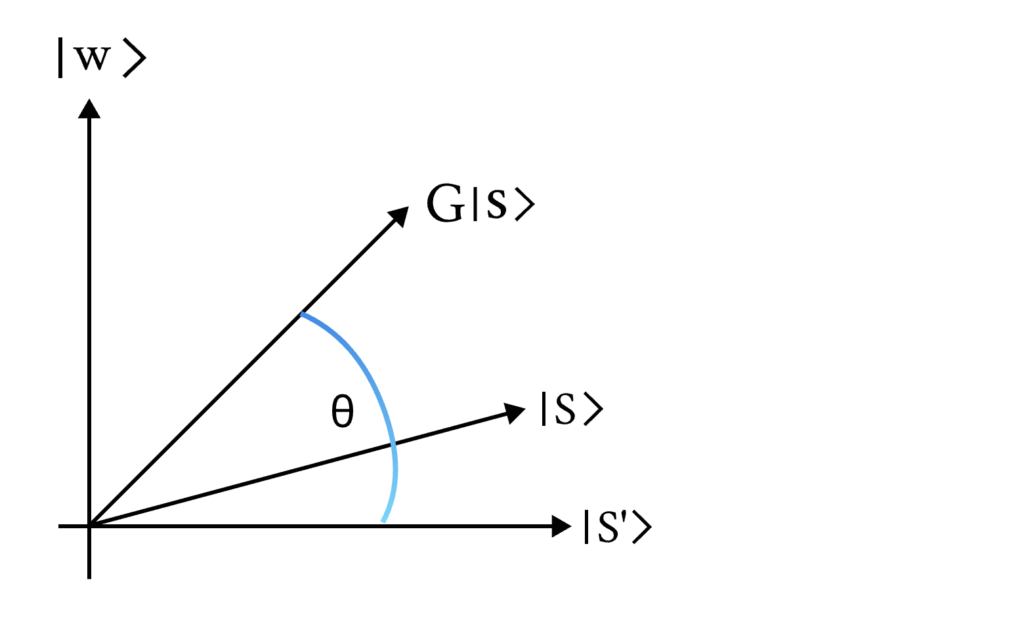
搜索空间中的解的百分比影响 |s\rangle 和 |s’\rangle 之间的差异。例如,如果没有很多解, |s\rangle 会非常接近 |s’\rangle,而 \theta 会非常小。事实证明,Grover 迭代器的特征值是 e^{\pm i\theta},我们可以使用量子相位估计 (QPE) 来提取这个值,从而估计解的数量 ( M )。
1.2 深入探讨
在 |\omega\rangle,|s’\rangle 基下,我们可以将 Grover 迭代器写成矩阵形式:
G =
\begin{pmatrix}
\cos{\theta} && -\sin{\theta}\\
\sin{\theta} && \cos{\theta}
\end{pmatrix}
矩阵 G 有特征向量:
\begin{pmatrix}
-i\\
1
\end{pmatrix}
,
\begin{pmatrix}
i\\
1
\end{pmatrix}
对应的特征值为 e^{\pm i\theta}。我们不需要将寄存器准备这两个状态中的任何一个,状态 |s\rangle 位于 |\omega\rangle, |s’\rangle 张成的空间中,是两个向量的叠加态。
|s\rangle = \alpha |\omega\rangle + \beta|s’\rangle
因此, QPE 算法的输出将是两个相位的叠加,当我们测量寄存器时,将获得这两个值中的一个。我们可以使用一些简单的数学运算来估计 M 。
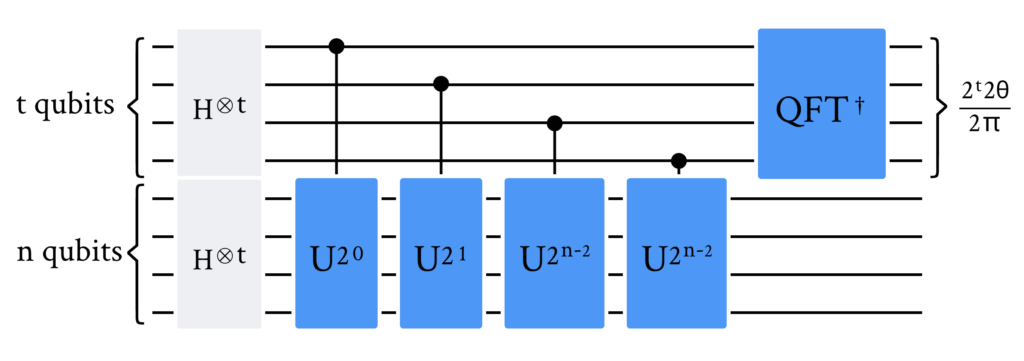
2. 代码实现
2.1 初始化代码
我们选择在线路的前 4 个量子比特上进行”计数”(我们将计数量子比特数称为 t ,所以 t = 4 ),并在最后 4 个量子比特上进行”搜索”( n = 4 )。基于此,我们可以开始创建量子线路的构建块。
2.2 受控 Grover 迭代
Grover 算法中有一个我们知道有 5 个解 ( M = 5 ) 的 16 个态 ( N = 2^n = 16 ) 的 Oracle,与扩散算子结合使用:
import deepquantum as dq
def example_grover_iteration():
"""Small circuit with 5/16 solutions"""
# Do circuit
cir = dq.QubitCircuit(4)
# Oracle
cir.h(2)
cir.h(3)
cir.ccx(0,1,2)
cir.h(2)
cir.x(2)
cir.ccx(0,2,3)
cir.x(2)
cir.h(3)
cir.x(1)
cir.x(3)
cir.h(2)
cir.x(2,[0,1,3])
cir.x(1)
cir.x(3)
cir.h(2)
# Diffuser
cir.hlayer([0,1,2])
cir.xlayer([0,1,2])
cir.z(3)
cir.x(3,[0,1,2])
cir.xlayer([0,1,2])
cir.hlayer([0,1,2])
cir.z(3)
return cir
我们可以使用 .get_unitary() 和 .any 从量子线路创建一个受控门。我们将 Grover 迭代器称为 grit:
# Create controlled-Grover
grit = example_grover_iteration().get_unitary()
cir_test = dq.QubitCircuit(5)
cir_test.any(unitary=grit,wires=[1,2,3,4],controls=0,name="_Grover")
cir_test.draw()
2.3 逆量子傅里叶变换
我们现在需要创建一个逆量子傅里叶变换。我们使用 t = 4 个量子比特创建这个门,因为这是我们在本案例中选择的计数量子比特数。
qft = dq.QuantumFourierTransform(nqubit=4, minmax=[0, 3], reverse=True).inverse()
qft.draw()
2.4 组合量子线路
我们现在已经拥有完成线路所需的一切!让我们把它组合在一起。
# 创建量子电路
t = 4 # 计数量子位的数量
n = 4 # 搜索量子位的数量
cir = dq.QubitCircuit(n+t) # 一个包含 n+t 个量子位和 t 个经典位的电路
# 初始化所有量子位到 |+>
cir.hlayer()
# 开始受控Grover迭代
iterations = 1
for qubit in range(t):
for i in range(iterations):
cir.any(unitary=grit,wires=list(range(t, n+t)),controls=qubit,name="_Grover")
iterations *= 2
# 在计数量子位上执行逆量子傅里叶变换
cir.barrier()
cir.add(dq.QuantumFourierTransform(nqubit=n+t, minmax=[0,t-1], reverse=True).inverse())
# 测量计数量子位
cir.barrier()
cir.measure(wires=list(range(t)))
# 显示电路图
cir.draw()
c:\Users\HP\.conda\envs\dq\lib\site-packages\qiskit\visualization\circuit\matplotlib.py:266: FutureWarning: The default matplotlib drawer scheme will be changed to "iqp" in a following release. To silence this warning, specify the current default explicitly as style="clifford", or the new default as style="iqp".
self._style, def_font_ratio = load_style(self._style)

cir()
res = cir.measure(wires=list(range(t)))
print(res)
{'1011': 510, '0101': 514}
import matplotlib.pyplot as plt
# 将数据分解为X和Y轴的值
labels = list(res.keys())
values = list(res.values())
# 创建条形图
plt.figure(figsize=(8, 5)) # 设置图形大小
plt.bar(labels, values) # 绘制条形图

3. 仿真结果
我们可以看到有两个值特别突出,具有比其他值高得多的测量概率。这两个值对应于 e^{i\theta} 和 e^{-i\theta},但我们还看不到解的数量。我们需要再做一些处理才能得到这个信息。
我们将从输出数据中获取最可能结果的字符串,再将其存储为整数:
measured_str = max(res, key=res.get)
measured_int = int(measured_str,2)
print("Register Output = %i" % measured_int)
Register Output = 5
4. 求解的数量 (M)
首先,我们要从 measured_int 中得到 \theta。你会记得 QPE 给我们一个测量值 \text{value} = 2^n \phi,来自特征值 e^{2\pi i\phi},所以为了得到 \theta,我们需要:
\theta = \text{value}\times\frac{2\pi}{2^t}
我们可以从 |s\rangle 和 |s’\rangle 的内积中得到角度 \theta/2:
\langle s’|s\rangle = \cos{\tfrac{\theta}{2}}
并且 |s\rangle (计算基态的均匀叠加) 可以用 |\omega\rangle 和 |s’\rangle 来表示:
|s\rangle = \sqrt{\tfrac{M}{N}}|\omega\rangle + \sqrt{\tfrac{N-M}{N}}|s’\rangle
|s\rangle 和 |s’\rangle 的内积是:
\langle s’|s\rangle = \sqrt{\frac{N-M}{N}} = \cos{\tfrac{\theta}{2}}
易知:
N\sin^2{\frac{\theta}{2}} = M
量子计数算法将告诉我们有多少状态不是解。我们简单地计算 N-M 。
用代码表示:
import math
theta = (measured_int/(2**t))*math.pi*2
N = 2**n
M = N * (math.sin(theta/2)**2)
print("No. of Solutions = %.1f" % (N-M))
No. of Solutions = 4.9
我们可以看到,我们得到了(近似)正确的答案,我们可以使用以下公式近似计算这个答案的误差[1]:
m = t - 1 # Upper bound: Will be less than this
err = (math.sqrt(2*M*N) + N/(2**(m+1)))*(2**(-m))
print("Error < %.2f" % err)
Error < 2.48
5. 参考文献
[1] Nielsen M A, Chuang I L. Quantum computation and quantum information[M]. Cambridge university press, 2010.


