![]()
1. 算法背景
非线性微分方程组在自然科学和工程领域中扮演着关键的角色,用于描述一系列复杂的现象和问题,包括Navier-Stokes方程、等离子体流体动力学和流行病学等。这些方程组的求解对于理解自然现象、优化系统性能和解决实际问题至关重要。变分量子算法是一类利用经典优化器来训练含参量子线路的算法,它们可以用来求解哈密顿量的本征值、组合优化问题、机器学习问题等。变分量子算法的基本思想是,通过调整量子线路中的参数,使得某个损失函数达到最小值,从而得到问题的最优解或者近似解。变分量子算法的优势在于,它们只需要较少的量子资源,适合在带噪声的中型量子计算机上运行。这里我们基于DeepQuantum定制化开发了一个变分量子算法来求解非线性常微分方程组,并以Navier-Stokes方程的收敛-发散喷嘴问题作为一个具体例子进行了演示。
Navier-Stokes方程可以写作以下形式:
其中:
– \mathbf{u} 是流体的速度向量,依赖于时间 t 和空间位置。
– \rho 是流体的密度。
– p 是流体的压强。
– \nu 是动力粘性系数,它描述了流体内部的粘滞性。
– \mathbf{f} 是作用在流体上的体积力(如重力)。
方程解释
- 时间导数 \frac{\partial \mathbf{u}}{\partial t} 表示流体速度随时间的变化。
- 对流项 (\mathbf{u} \cdot \nabla) \mathbf{u} 表示流体因其速度场的非均匀分布而导致的自身运动的影响。
- 压力梯度 -\frac{1}{\rho} \nabla p 说明压力的变化驱动流体运动。
- 粘性项 \nu \nabla^2 \mathbf{u} 描述了流体内部的摩擦力对流体运动的影响。
- 体积力 \mathbf{f} 是外部力如重力或电磁力的作用。
2. 收敛-发散喷嘴问题
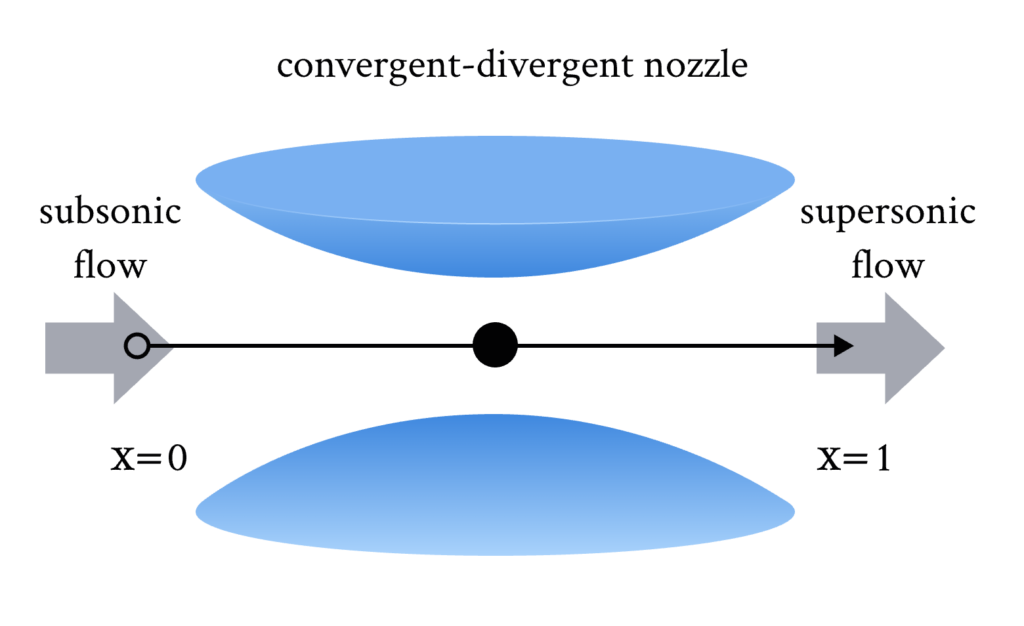
这个问题即要求一维流体经过上图所示的结构,然后计算流体流动的密度、温度和速度分布,具体的方程组如下所示 [1]:
为了进一步简化问题,我们考虑稳态情况的解,即有:
\frac{dp}{dx} = \frac{\rho V^2}{T – V^2} d_x(\ln A),
\frac{dT}{dx} = \frac{TV^2(\gamma – 1)}{T – V^2} d_x(\ln A), \\
\frac{dV}{dx} = -\frac{TV}{T – V^2} d_x(\ln A).
这里的A(x)描述了喷嘴的形状。
3. 算法原理
将变量x通过角度编码加入参数化量子线路(parameterized quantum circuit,PQC)后,可以通过测量得到指定可观测量的期望值。这就实现了一个可变分的函数映射。并且当PQC对变量x进行角度编码时,可以通过参数位移法得到变量x的精确梯度,于是利用这种可微量子线路(differentiable quantum circuit,DQC),把函数项与导数项联系起来后,就可以自然地求解常微分方程。总体流程图包含确定输入、初始化量子线路、优化量子线路以及终止条件。
在输入方面,主要是确定要求解的微分方程(组)和边界条件。在初始化量子线路方面,可以选择不同的变分拟设(ansatz),选择不同的特征映射函数,选择不同的代价函数、损失函数以及选择不同的处理边界条件的方法。在优化量子线路方面,通过采用混合量子-经典的工作流,对DQC进行训练,以满足微分方程和指定的边界条件。最后当损失函数收敛到一定阈值或者训练轮数到达指定值时,结束训练。
具体到这个案例,我们利用经典的非线性激活函数设计了一个量子特征映射,使得对于输入而言相当于引入了Chebyshev多项式,直观理解就是量子比特越多,拟合函数所使用的Chebyshev多项式的阶数越高。该映射提供了一个强大的拟合多项式的基函数集合,并具有丰富的表达能力。对于边界条件的处理,通过floating boundary handling,即对期望值加一个常数来作为预测值,在每次迭代中都调整这个常数使得预测值满足边界条件,可以完美处理单边的边界条件。更多细节我们将结合代码进行说明。
总的来说,变分量子算法对于非线性特征映射、线路结构、测量期望值等选择是多种多样的,同时优化过程中,需要根据具体问题的特点选择合适的优化策略以及相关超参数,大家可以自行进行相关探索。
4. 代码实现
DQC类根据指定的量子比特数和层数来进行初始化,并且可以指定量子特征映射的形式,比如内置了”chebyshev”和”chebyshev_tower”两种,我们也可以将自定义的量子特征映射加入”nonlinear”。
“circuit”函数用于构建量子线路的结构,这里默认第一层Ry作为数据编码层(由encode参数指定),然后由一层Rz一层Rx一层Rz再加两层交错的CNOT作为变分层并且可以多次重复。用户也可以在这里构建自定义的量子线路。如果没有指定可观测量的个数,则默认对每个量子比特做z测量。
“get_observable”函数根据量子线路的比特数以及所需的可观测量的个数,返回一个包含一系列可观测量的列表。
“forward”函数实现前向计算过程,经典数据经过量子特征映射以及量子线路的演化,所得到的可观测量期望值之和即作为输出。
import deepquantum as dq
import matplotlib.pyplot as plt
import numpy as np
import torch
import torch.nn as nn
from tqdm import tqdm
# 变分量子算法
class DQC(nn.Module):
def __init__(self, nqubit, nlayer, nob=None, feat_map='chebt'):
super().__init__()
# 初始化量子位个数、层数、观测数和特征映射
self.nqubit = nqubit
self.nlayer = nlayer
self.nob = nob
self.feat_map = feat_map
# 构建量子线路
self.cir = self.circuit(nqubit, nlayer, nob)
# 定义chebyshev特征映射(第一类)
def chebyshev(self, x):
phi = []
for _ in range(self.nqubit):
# 对每个量子位应用切比雪夫变换
phi.append(2 * torch.arccos(x))
return torch.cat(phi, dim=-1)
# 定义chebyshev_tower特征映射
def chebyshev_tower(self, x):
phi = []
for i in range(self.nqubit):
# 变化频率随量子位位置增加
phi.append(2 * (i + 1) * torch.arccos(x))
return torch.cat(phi, dim=-1)
# 根据选择的特征映射类型应用非线性变换
def nonlinear(self, x):
if self.feat_map == 'cheb':
return self.chebyshev(x)
if self.feat_map == 'chebt':
return self.chebyshev_tower(x)
# 构建量子线路
def circuit(self, nqubit, nlayer, nob):
# 初始化量子线路
cir = dq.QubitCircuit(nqubit)
# 添加编码层
cir.rylayer(encode=True)
for _ in range(nlayer):
# 对于每层添加旋转和受控非门
cir.rzlayer()
cir.rylayer()
cir.rzlayer()
wires = list(range(nqubit))
# 添加交错的受控非门
for i in wires[1::2]:
cir.cnot(i - 1, i)
for i in wires[2::2]:
cir.cnot(i - 1, i)
# 根据是否指定观测设备添加观测
if nob is None:
for i in range(nqubit):
cir.observable(i)
else:
obs = DQC.get_observable(nqubit, nob)
for ob in obs:
cir.observable(wires=ob['wires'], basis=ob['basis'])
return cir
@staticmethod
def get_observable(nqubit, nob):
"""获取所有可能的观测量。
"""
assert nob < 4 ** nqubit # 确保提供的观测量数量不超过最大可能数量
ob_lst = []
bit_ob = {'00': 'i', '01': 'x', '10': 'y', '11': 'z'} # 定义比特到观测基的映射
# 每个观测量由一个数字表示
num = 1
while num <= nob:
wires = [] # 要作用的量子比特线
basis = '' # 对应的Pauli基
bits = format(num, f'0{2 * nqubit}b') # 将数字转换成二进制格式,长度为2*nqubit
for i in range(nqubit):
pauli = bit_ob[bits[2*i:2*i+2]] # 获取对应的Pauli操作
if pauli != 'i': # 如果操作不是恒等操作('i'),则记录下来
wires.append(i)
basis += pauli
ob = {'wires': wires, 'basis': basis} # 创建一个观测量的字典
ob_lst.append(ob) # 添加到列表中
num += 1
return ob_lst
def forward(self, x):
"""前向传播函数,用于神经网络模型中。
"""
x = torch.arctan(x) # 对输入数据应用反正切函数作为预处理
x = self.nonlinear(x) # 应用非线性函数处理数据
self.cir(x) # 使用预设的量子电路对数据进行处理
exp = self.cir.expectation() # 获取量子电路的期望值
out = exp.sum(dim=-1, keepdim=True) # 对期望值进行求和,以生成最终的输出张量
return out
NavierStokes类实现对处理问题方式的建模,用户可以指定DQC的信息,以及Navier-Stokes方程的收敛-发散喷嘴问题中的单边边界条件,包括对边界条件的处理方法。这里的’float’即代表上面介绍的floating boundary的处理方式。”forward”函数实现具体的函数拟合,给定坐标x,返回密度、温度和速度。
“loss_ns_stationary_conv_div_nozzle” 函数实现根据要求解的常微分方程组来构建损失函数。具体而言,对于目前这个案例,所采用的喷嘴的形状为:
所要求解的常微分方程组为:
\frac{dp}{dx} = \frac{\rho V^2}{T – V^2} d_x(\ln A),
\frac{dT}{dx} = \frac{TV^2(\gamma – 1)}{T – V^2} d_x(\ln A),
\frac{dV}{dx} = -\frac{TV}{T – V^2} d_x(\ln A).
代码与方程是对应的.
“loss_reg_ns_stationary_conv_div_nozzle”函数实现根据指定的预期目标来返回正则项。
整个训练过程包含了两个阶段的训练。我们需要输入待训练的模型、训练集数据、正则项数据、损失函数和正则项的形式、要使用的优化器、迭代轮数、控制正则项衰减的超参数以及运行设备。训练完返回训练好的模型以及训练过程中记录的损失函数情况。
class NavierStokes(nn.Module):
def __init__(self, nqubit, nlayer, x0, rho0, tem0, vel0, feat_map='cheb', bound='float'):
super().__init__()
self.nqubit = nqubit
self.nlayer = nlayer
self.feat_map = feat_map
self.bound = bound
self.rho = DQC(nqubit, nlayer, feat_map=feat_map)
self.tem = DQC(nqubit, nlayer, feat_map=feat_map)
self.vel = DQC(nqubit, nlayer, feat_map=feat_map)
x0 = x0.reshape(-1, 1)
self.register_buffer('x0', x0)
self.rho0 = rho0
self.tem0 = tem0
self.vel0 = vel0
def forward(self, x):
rho = self.rho(x)
tem = self.tem(x)
vel = self.vel(x)
if self.bound == 'float':
rho += self.rho0 - self.rho(self.x0).detach().clone()
tem += self.tem0 - self.tem(self.x0).detach().clone()
vel += self.vel0 - self.vel(self.x0).detach().clone()
return rho, tem, vel
def loss_ns_stationary_conv_div_nozzle(model, x, criterion):
gamma = 1.4
d_ln_a = (19.8 * (2 * x - 1)) / (1 + 4.95 * (2 * x - 1) ** 2)
rho, t, v = model(x)
v2 = v ** 2
drho = torch.autograd.grad(rho, x, grad_outputs=torch.ones_like(rho), create_graph=True)[0]
dt = torch.autograd.grad(t, x, grad_outputs=torch.ones_like(t), create_graph=True)[0]
dv = torch.autograd.grad(v, x, grad_outputs=torch.ones_like(v), create_graph=True)[0]
labels = torch.zeros_like(x, device=x.device)
loss_rho = criterion(drho - rho * v2 * d_ln_a / (t - v2), labels)
loss_tem = criterion(dt - t * v2 * (gamma - 1) * d_ln_a / (t - v2), labels)
loss_vel = criterion(dv + t * v * d_ln_a / (t - v2), labels)
return loss_rho + loss_tem + loss_vel
def loss_reg_ns_stationary_conv_div_nozzle(model, x_reg, rho_reg, tem_reg, vel_reg, criterion):
rho, tem, vel = model(x_reg)
loss_rho = criterion(rho, rho_reg)
loss_tem = criterion(tem, tem_reg)
loss_vel = criterion(vel, vel_reg)
return loss_rho + loss_tem + loss_vel
def train(model, x_train1, x_train2, x_reg, criterion, criterion_reg, optimizer1, optimizer2,
niter1, niter2, delta, device):
model = model.to(device)
x_train1 = x_train1.to(device)
x_train2 = x_train2.to(device)
x_reg = x_reg.to(device)
l_stage1 = []
l_stage2_full = []
l_stage2_diff = []
for i in tqdm(range(niter1)):
optimizer1.zero_grad()
loss = loss_ns_stationary_conv_div_nozzle(model, x_train1, criterion)
loss.backward()
optimizer1.step()
l_stage1.append(loss.item())
rho_reg, tem_reg, vel_reg = model(x_reg)
rho_reg = rho_reg.detach().clone()
tem_reg = tem_reg.detach().clone()
vel_reg = vel_reg.detach().clone()
for i in tqdm(range(niter2)):
optimizer2.zero_grad()
loss_diff = loss_ns_stationary_conv_div_nozzle(model, x_train2, criterion)
sche = 1 - np.tanh((i + 1) / (delta * niter2))
loss = loss_diff + sche * loss_reg_ns_stationary_conv_div_nozzle(model, x_reg, rho_reg, tem_reg, vel_reg, criterion_reg)
loss.backward()
optimizer2.step()
l_stage2_full.append(loss.item())
l_stage2_diff.append(loss_diff.item())
result = {'loss_stage1': l_stage1, 'loss_stage2_full': l_stage2_full, 'loss_stage2_diff': l_stage2_diff}
return model, result
这里统一列出了与训练过程相关的一些参数。我们还可以修改模型、损失函数和正则项的形式以及优化器的相关信息。比如这里默认使用了6个量子比特和6层线路结构,默认的边界条件为:
确定好所有参数后运行
x1 = 0 # 第一段空间的起点
x2 = 0.4 # 第一段空间的终点
x3 = 0.6 # 第二段空间的起点
x4 = 0.9 # 第二段空间的终点
nstep1 = 20 # 第一段空间的点数
nstep_reg1 = 20 # 第一段空间的正则项所用的点数
nstep2 = 20 # 第二段空间的点数
nstep_reg2 = 5 # 第二段空间的正则项所用的点数
niter1 = 200 # 一阶段训练迭代次数
niter2 = 600 # 二阶段训练迭代次数
delta = 1 / 8 # 控制正则项衰减的超参数
device = 'cpu'
x_train1 = torch.linspace(x1, x2, nstep1, requires_grad=True).reshape(-1, 1)
x_train2 = torch.linspace(x3, x4, nstep2, requires_grad=True).reshape(-1, 1)
x_reg1 = torch.linspace(x1, x2, nstep_reg1).reshape(-1, 1)
x_reg2 = torch.linspace(x3, x4, nstep_reg2).reshape(-1, 1)
x_train = torch.cat([x_train1, x_train2], dim=0)
x_reg = torch.cat([x_reg1, x_reg2], dim=0)
x_test = torch.linspace(x1, x4, 100).reshape(-1, 1)
model = NavierStokes(6, 6, x_train[0, 0], 1, 1, 0.1)
criterion = nn.MSELoss()
criterion_reg = nn.MSELoss(reduction='sum')
optimizer1 = torch.optim.Adam(model.parameters(), lr=0.01, betas=(0.9, 0.999))
optimizer2 = torch.optim.Adam(model.parameters(), lr=0.005, betas=(0.9, 0.999))
model, rst = train(model, x_train1, x_train, x_reg, criterion, criterion_reg, optimizer1, optimizer2, niter1, niter2, delta, device)
l_stage1 = rst['loss_stage1']
l_stage2_full = rst['loss_stage2_full']
l_stage2_diff = rst['loss_stage2_diff']
plt.plot(l_stage1)
plt.xlabel('n')
plt.ylabel('loss')
plt.yscale('log')
plt.grid()
plt.tight_layout()
plt.clf()
plt.plot(l_stage2_diff, label='L_{D}')
plt.plot(l_stage2_full, label='L_{F}')
plt.xlabel('n')
plt.ylabel('loss')
plt.yscale('log')
plt.grid()
plt.legend()
plt.tight_layout()
plt.clf()
rho, tem, vel = model(x_test)
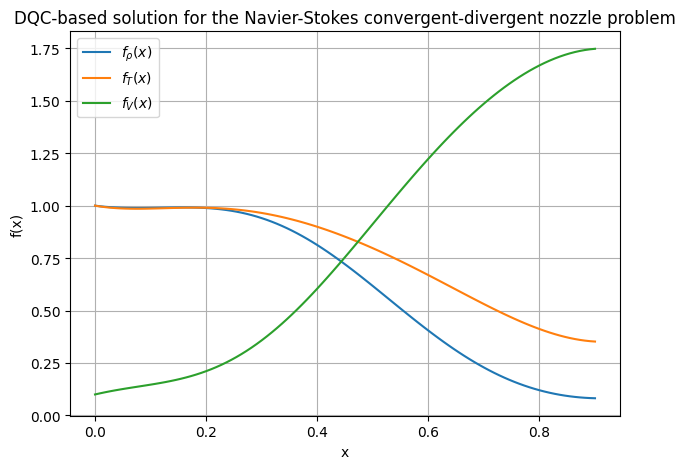
plt.plot(x_test.numpy(), rho.detach().numpy(), label=r'f_{\rho}(x)')
plt.plot(x_test.numpy(), tem.detach().numpy(), label=r'f_{T}(x)')
plt.plot(x_test.numpy(), vel.detach().numpy(), label=r'f_{V}(x)')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('DQC-based solution for the Navier-Stokes convergent-divergent nozzle problem')
plt.grid()
plt.legend()
plt.tight_layout()
100%|██████████| 200/200 [02:16<00:00, 1.46it/s]
100%|██████████| 600/600 [13:07<00:00, 1.31s/it]
C:\Users\HP\AppData\Local\Temp\ipykernel_255840\2446350459.py:48: UserWarning: The figure layout has changed to tight
plt.tight_layout()
C:\Users\HP\AppData\Local\Temp\ipykernel_255840\2446350459.py:60: UserWarning: The figure layout has changed to tight
plt.tight_layout()
5. 参考文献
[1] Kyriienko, O., Paine, A. E., & Elfving, V. E. (2021). Solving nonlinear differential equations with differentiable quantum circuits. Physical Review A, 103(5), 052416.


