![]()
高斯玻色采样应用到稠密子图问题
- 图和子图
数学上图 G 的定义如下:
集合V中的元素称为节点,集合E中的元素时两个节点组成的无序对,称为边。集合V称为点集,E称为边集。在图的定义中边的概念定义了节点上的一个对称关系,即邻接关系(adjacency relation)。对于两个节点 x,y,如果 (x,y) 是一条边,则称他们是邻接的,因此一张图可以用一个 n\times n 的邻接矩阵A来表示。比如对于四个节点的全连接图对应的A如下。
haf(A) = 3, 表示完美匹配数为3。
子图对应的点集和边集分别是图G的点集的子集和边集的子集,稠密子图直观上对应着连接密集的子图,图密度的定义如下
|E| 表示对应的边的条数,|V| 表示对应的节点个数。
那么稠密子图就对应着图密度很大的子图。
- GBS采样和稠密子图
参考文献[1]中讨论了图 G 的完美匹配数和图密度 d(G) 的关系,hafnian的计算对应图 G 的完美匹配数,那么hafnian值越大那么图的稠密度越高。由前面讨论可知高斯玻色采样下hafnian值越大也对应着采样概率越高,即概率越高的样本对应的子图的稠密度越大。在使用粒子数分辨探测器时,通过后选择对采样的样本筛选出只有0,1的结果,这些结果中出现概率较高的Fock态所映射的子图就对应了稠密子图。同时还可以用经典算法来寻找稠密子图,这里用到的经典算法如下,
a. 选择子图规模大小 [k_{min},k_{max}]。
b. 子图规模从大到小搜索(shrinking),从全图开始,对于 k>k_{min},每次搜索随机删除一个连接数最少的节点,剩下的节点组合成当前规模下的稠密子图。
c. 子图规模从小到大搜索(growth),对于 k<k_{max},每次搜索随机添加一个连接数最多的节点,组成当前规模下的稠密子图。
代码演示
import deepquantum.photonic as dqp
import networkx as nx
import torch
from collections import defaultdict
from strawberryfields.apps.subgraph import resize
经典算法
这里采用下图数据中16个节点的图作为例子,这个图可以看作是两部分子图组成,一部分是较为稀疏的子图,对应节点为0到9,另一部分是稠密的子图,对应的节点为10到15。我们的目标是找到包含6个节点的稠密子图,即[10,11,12,13,14,15]组成的子图。
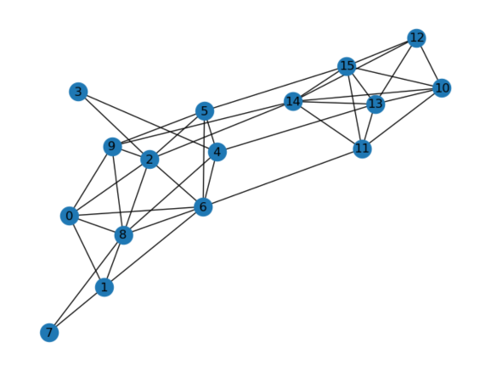
这里的经典算法是基于贪心算法实现的,即每一次迭代寻找连接数最少的那个节点然后移除就可得到当前规模下的稠密子图, 但是如果有多个节点的连接数相同,那么它会随机选择一个节点移除,这就导致了目标稠密子图包含的节点有可能被移除,最终导致得到的结果有偏差。
a = dqp.utils.load_adj('densegraph_adj')
graph = nx.from_numpy_array(a)
s = range(16)
r = resize(s, graph, min_size=1, max_size=15)
r[6], nx.density(graph.subgraph(r[6]))
([10, 11, 12, 13, 14, 15], 0.9333333333333333)
量子-经典混合算法
量子-经典混合算法中先通过高斯玻色采样得到概率较高的样本然后转化成对应的子图,这些子图可以作为经典算法的搜索起点,可以有效的提高最后结果的准确度。
这里先读取已有的高斯玻色采样数据,采样次数为十万次,gbs.postselect 函数先挑出那些对应子图节点数为8、10的样本,然后将这些样本子图作为经典搜索算法的起点,可以得到一个最终收敛到节点为6的子图字典。字典中包含了节点数为6的图密度较大的多个子图, 我们取图密度最大的那个子图就是最终的结果。
def search_subgpraph(samples: list,
graph: nx.Graph,
min_size: int,
max_size: int):
"""Get the densest subgraph with size in [min_size, max_size],
using classical algorithm with samples from GBS
"""
dic_list = defaultdict(list)
for i in range(len(samples)):
temp= samples[i]
num = 1
for key in temp.keys():
if num < 50: # only need 50 samples
idx = torch.nonzero(torch.tensor(key)).squeeze()
r = resize(idx.tolist(), graph, min_size=min_size, max_size=max_size)
for j in range(min_size, max_size+2, 2):
density = nx.density(graph.subgraph(r[j]))
temp_value = (r[j], np.round(density, 5))
if temp_value not in dic_list[j]:
dic_list[j].append(temp_value)
num = num + 1
return dic_list
# 后处理得到节点数为8和10个子图对应的样本
sample_re = dqp.utils.load_sample('densegraph_sample')
gbs = dqp.GBS_Graph(adj_mat=torch.tensor(a, dtype = torch.float64), cutoff=2)
state = gbs()
subgraph_sample = gbs.postselect(sample_re, [8, 10])
# 采用shrinking 方法得到节点数为6和8的稠密子图
dense_sub_graph = search_subgpraph(subgraph_sample, graph, min_size=6, max_size=8)
print(dense_sub_graph[6][0])
([10, 11, 12, 13, 14, 15], 0.93333)
量子算法
量子算法直接将高斯玻色采样后的6个节点对应的样本挑选出来处理,因为根据前面的讨论可以知道,对应的子图越稠密那么其样本出现的概率也就越大。这里先读取已有的高斯玻色采样数据,采样次数为十万次,gbs.postselect 函数先挑出那些对应子图节点数为6的样本,然后gbs.graph_density 函数将这些样本映射成子图再计算子图的图密度,最后按图密度从大到小排列给出对应的子图及其图密度。从最后的结果可以看到,高斯玻色采样成功采到了图密度最高的6个节点的子图,对应的图密度为0.9333,对应的节点为[10,11,12,13,14,15]。
sample_re = dqp.utils.load_sample('densegraph_sample')
subgraph_sample = gbs.postselect(sample_re, [6])
subgraph_density = gbs.graph_density(graph, subgraph_sample[0])
key = list(subgraph_density.keys())
print(key[0],subgraph_density[key[0]])
(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1) [tensor([144]), 0.9333333333333333]
附录
[1] J. M. Arrazola and T. R. Bromley, Physical Review Letters 121, 030503 (2018).


