量子态层析

量子态层析（Quantum State Tomography, QST）是一种用于测量和重构量子系统密度矩阵的技术。其主要目的是通过实验测量获得的信息来推断出一个量子态的完全描述。在量子计算和量子信息处理中，量子态层析是一项关键技术，因为它提供了验证和分析量子系统状态的手段。量子态可以通过密度矩阵 $\rho$ 完全描述。在d-维希尔伯特空间中，一个纯量子态可以用一个 $(d \times d)$ 的密度矩阵来表示，量子态层析的目标是通过一系列的测量结果来重构这个密度矩阵。

对于一个 n-量子比特系统，密度矩阵是一个 $2^n \times 2^n$ 的矩阵。一般通过进行一系列的投影测量（比如泡利矩阵的张量积）来获得关于量子态的信息。每个测量结果对应于密度矩阵的特定线性组合。使用测量结果构建一组线性方程，解决这些方程来重构密度矩阵。

在得到重构的密度矩阵之后可以计算任意算符的期望，同时也可以通过特定的测量值来计算任意算符的期望。因此重构密度矩阵的任务和计算任意算符期望的任务是等价的。比如一个光量子单模线路中，量子态用Fock基矢表示如下： $|\psi\rangle = \sum_i a_i |i\rangle$ ，对于密度矩阵 $\rho$ 的分量 $\rho_{ij} = \langle i |\rho|j\rangle = a_ia_j^*$ , 同时在量子态下 $|\psi\rangle$ 测量算符 $|j\rangle\langle i|$ 得到的期望也是 $a_ia_j^*$ ，因此重构密度矩阵等价于测量对应算符的期望。

平衡零拍测量

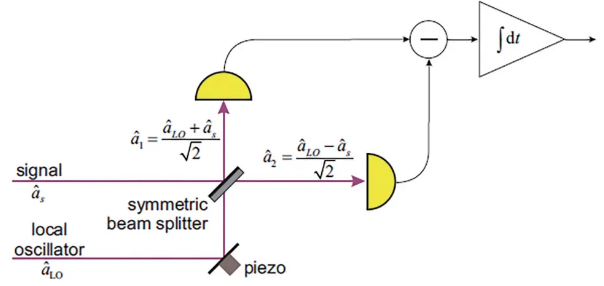
量子光学实验中可以测量光场量子态正交分量值的探测方法称为平衡零拍探测（Homodyne测量）[1]。其基本原理如下图所示，一束待测信号光场与一束同频的强本振光（LO）在 50/50 光学分束器合束，分束器之后的两束光分别进入两个相同的光电探测器，随后两个输出的光电流信号经减法器相减，输出的光电流信号正比于信号光场的正交分量值。
$i_{out}(t) \sim X_\theta(t)$
$X_\theta = X cos\theta + P sin\theta$ ， $X, P$ 对应于算符 $\hat{x}, \hat{p}$ 的本征值， $\theta$ 对应分束器的可调角度。

在光量子系统中由于量子系统很脆弱，经过探测之后就会被破坏，因此为了获得量子态在不同正交分量值下的几率分布就需要制备很多份全同的量子态。量子层析的基本过程是首先在不同正交相位角 $\theta$ 下测量未知量子态的正交分量值，然后对其进行统计求得 $X_\theta$ 对应的正交分量概率分布 $Pr(X_\theta)$ ，之后可以用最大似然估计算法推断出最有可能满足这一系列正交分量几率分布的量子态的密度矩阵与Wigner函数，也可以通过用这些概率分布来计算对应算符的期望。

单模线路量子态层析

理论基础

给定一个算符，一般会考虑用算符基矢展开，光量子计算中可以将位移算符 $D(\alpha) = e^{\alpha a^\dagger – \alpha^* a}$ 作为一组正交完备的算符基矢, 那么作用在希尔伯特空间的任意算符 $A$ 都可以用这一组基矢展开[2]。

$A=\int_{\mathbb{C}}\frac{d^2\alpha}{\pi} \mathrm{Tr}[A \mathcal{D}^\dagger(\alpha)]\mathcal{D}(\alpha)=\int_{0}^{\pi}\frac{d\phi}{\pi}\int_{-\infty}^{+\infty}dr\frac{|r|}{4}\mathrm{Tr}[A e^{irX_\phi}]e^{-irX_\phi}$

这里算符的内积用trace来定义, $\langle A|B\rangle = Tr[A^\dagger B]$ 。采用极坐标参数 $\alpha = -ir e^{i\phi/2}$ 。正交分量 $X_\phi$ 的定义如下：
$X_\phi=(a^\dagger e^{i\phi}+ae^{-i\phi})/2$
那么观测量 $\langle A \rangle$ 的表示如下：

$\begin{aligned} \left\langle A\right\rangle & =Tr(A\rho) \\\\ &=Tr(\int\frac{d^2\alpha}\pi Tr(AD^\dagger(\alpha))D(\alpha)\rho) \\\\ &=\int_0^\pi\frac{d\phi}\pi\int_{-\infty}^\infty dr\frac{|r|}4Tr(Ae^{irX_\phi})Tr(\rho e^{-irX_\phi}) \\\\ &=\int_{0}^{\pi}\frac{d\phi}{\pi}\int_{-\infty}^{\infty}dx\int_{-\infty}^{\infty}dr\frac{|r|}{4}Tr(Ae^{irX_{\phi}})p(\phi,x)e^{-irx} \\\\ &=\int_0^\pi\frac{d\phi}\pi\int_{-\infty}^\infty dxp(\phi,x)\int_{-\infty}^\infty dr\frac{|r|}4Tr(Ae^{ir(X_\phi-x)}) \\\\ &=\int_0^\pi\frac{d\phi}\pi\int_{-\infty}^\infty dxp(\phi,x)K(\phi,x,A) \end{aligned}$

这里 $p(\phi, x) = \langle X_\phi|\rho|X_\phi\rangle$ , 表示测量正交分量 $X_\phi$ 的分布，核函数 $K(\phi,x,A)$ 的定义如下：

$K_A(x,\phi)\equiv\int_{-\infty}^{+\infty}dr\frac{|r|}{4}\mathrm{Tr}[A e^{ir(X_\phi-x)}]$

对于单模情况的Fock基矢表示的算符 $A$ ( $A=|n+\lambda\rangle\langle n|$ ), 核函数的定义如下[3]：

$\begin{aligned}K(\phi,x,|n+\lambda\rangle\langle n|)&=2e^{-i\lambda\phi}\sqrt{\frac{n!}{(n+\lambda)!}}e^{-x^2}\sum_{\nu=0}^n\frac{(-1)^\nu}{\nu!}\left(\begin{array}{c}n+\lambda\\\\n-\nu\end{array}\right)\\\\ \times(2\nu+\lambda+1)!\operatorname{Re}\left[(-i)^\lambda\mathcal{D}_{-(2\nu+\lambda+2)}(-2ix)\right]\end{aligned}$

这里 $D_l(x)$ 是抛物线圆柱函数(parabolic cylinder funtion)，可以通过mpmath计算。

考虑单模情况下 $X_\phi$ 概率分布 $p(\phi, x)$ ， $X_\phi$ 可以化简

$X_\phi = \frac{1}{2}(\cos\phi(a^\dagger+a) + i\sin\phi(a^\dagger-a))=\frac{1}{2}(\cos\phi x_0 + \sin\phi p_0)$

$x_0$ , $p_0$ 的分布可以从边缘分布计算得到

$x_0 \sim N(\bar{x}_0, \sigma^2_{x_0}) \\\\ p_0 \sim N(\bar{p}_0, \sigma^2_{p_0})$

$X_\phi$ 对应的分布也是高斯分布，对应的平均值和方差如下

$\mu({X_\phi}) = \frac{1}{2}(\cos\phi \bar{x}_0 + \sin\phi \bar{p}_0), \\\\ \sigma({X_\phi}) = \frac{1}{4}(\cos^2\phi \sigma^2_{x_0}+\sin^2\phi \sigma^2_{p_0}) \\\\ p(X_\phi) \sim N(\frac{1}{2}(\cos\phi \bar{x}_0+\sin\phi \bar{p}_0), \frac{1}{4}(\cos^2\phi \sigma^2_{x_0}+\sin^2\phi \sigma^2_{p_0}))$

考虑多模的情况下， $\langle A_{M}\rangle$ 对应的二重积分变成多重积分，概率分布 $p(x, \phi)$ 变成联合概率分布 $p(x_1, \phi_1, x_2,\phi_2, …)$ ，核函数 $K(x, \phi, A)$ 变成 $K(x_1, x_2, … \phi_1, \phi_2,.., A)$ 。

$\begin{aligned}\langle A_{M}\rangle&=\int_{0}^{\pi}\frac{d\phi_{1}\cdots d\phi_{M}}{\pi^{M}}\int_{-\infty}^{+\infty}dx_{1}\cdots dx_{M} p(x_{1},\phi_{1},\cdots,x_{M},\phi_{M})\\\\\times K_{A_{M}}(x_{1},\phi_{1},\cdots,x_{M},\phi_{M}) ,\end{aligned}$

$K_{A_M}(x_1,\phi_1,\cdots)\equiv\int_{-\infty}^{+\infty}dr_1\cdots dr_M\prod_{m=1}^M\frac{|r_m|}{4}\mathrm{Tr}[A_M e^{ir_m(X_{\phi_m}-x_m)}]$

代码实现

下面以单模压缩态为例，计算算符 $|n+\lambda\rangle\langle n|$ 的平均值

import deepquantum as dq
import matplotlib.pyplot as plt
import torch

nmode = 1
cir = dq.QumodeCircuit(nmode=nmode, init_state='vac', cutoff=3, backend='gaussian')
cir.s(0, r=1)
state =cir()
probs = cir(is_prob=True)
cir.draw()

import numpy as np
import scipy
from scipy.special import factorial, comb
import mpmath
from mpmath import mp
mp.dps = 25; mp.pretty = True

def K_A(x, phi, n, labda):
    """
     Kernel function for calculating expetation value of |n+labda><n|
    """
    mp.dps = 15  # 设置mpmath的精度
    factor1 = 2 * np.exp(-1j * labda * phi) * np.exp(-x**2) * np.sqrt(factorial(n) / factorial(n+labda))
    sum_part = 0
    for j in range(n+1):
        term1 = (-1)**j / factorial(j) * comb(n + labda, n - j) * factorial(2*j + labda + 1)
        D_arg = -1* (2*j + labda + 2)
        D_val = mp.pcfd(D_arg, -2j * x) 
        real_part = mpmath.re((-1j)**(labda) * D_val)
        sum_part += term1 * real_part
    return np.array(complex(factor1 * sum_part))

def fun_(phi, x, n, labda, mu_x, mu_p, sigma_x, sigma_p):
    """
    calculating expectation value of operator |n+labda><n|
    """
    mu = (np.cos(phi)*(mu_x) + np.sin(phi)*(mu_p))/2
    sigma = (np.cos(phi)**2*sigma_x + np.sin(phi)**2*sigma_p)/4
    p_phi_x = 1/np.sqrt(2*np.pi*sigma)*np.exp(-(x-mu)**2/(2*sigma))
    kernel = K_A(x=x, phi=phi, n=n, labda=labda)
    return p_phi_x * kernel/np.pi

一般情况下 $\mu_x, \mu_p, \sigma_x, \sigma_p$ 是通过homodyne测量结果做统计学分析得到的，这里为了方便，直接用前向计算的结果代替homodyne测量结果。

sigma_x = np.array(state[0][0][0,0])
sigma_p = np.array(state[0][0][1,1])
mu_x = np.array(state[1][0][0])
mu_p = np.array(state[1][0][1])
sigma_x, sigma_p, mu_x, mu_p

(array(0.13533534, dtype=float32),
 array(7.3890557, dtype=float32),
 array([0.], dtype=float32),
 array([0.], dtype=float32))

考虑到核函数中包含 $e^{-x^2}$ 项，因此对于 $x$ 的数值积分上下限不需要取特别大，下面是计算 $|0\rangle\langle 0|$ 的期望，取不同上下限的结果，可以看到积分的结果很快就收敛, 并且和probs 中结果一致。

def fun_real(phi, x, n, labda, mu_x, mu_p, sigma_x, sigma_p):
    return fun_(phi, x, n, labda, mu_x, mu_p, sigma_x, sigma_p).real 
def fun_imag(phi, x, n, labda, mu_x, mu_p, sigma_x, sigma_p):
    return fun_(phi, x, n, labda, mu_x, mu_p, sigma_x, sigma_p).imag

for bound in range(0, 6):
    real_part = scipy.integrate.dblquad(fun_real, -bound,  bound, 0, np.pi, args=(0, 0, mu_x, mu_p, sigma_x, sigma_p))
    image_part = scipy.integrate.dblquad(fun_imag,-bound,  bound, 0, np.pi,  args=(0, 0, mu_x, mu_p, sigma_x, sigma_p))
    print('real', real_part, 'image',image_part)

real (0.0, 1.1407672702481792e-08) image (0.0, 0)
real (0.7384155086013756, 1.7029667227517772e-08) image (0.0, 0)
real (0.653721248196827, 1.8703001187493422e-08) image (0.0, 0)
real (0.6484413243208239, 1.8028299303789776e-08) image (0.0, 0)
real (0.6480760393870874, 1.8703001187493422e-08) image (0.0, 0)
real (0.648055115002439, 1.658743065951586e-08) image (0.0, 0)

但是对于多模的情况下，使用scipy进行多重积分的数值计算效率不高，这里我们介绍一种基于蒙特卡洛方法计算多重积分的数值方法。

蒙特卡洛方法计算多重积分

投点法

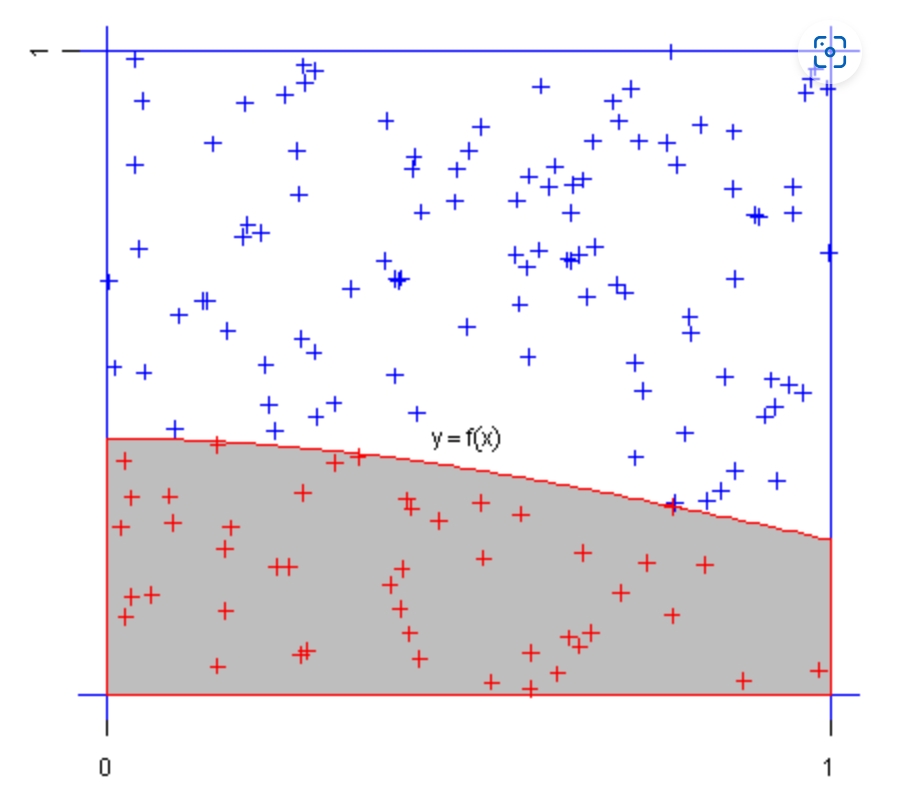
这里随机的点落在积分区域的概率正比于积分区域的面积，因此红点所占的比例乘以矩形的面积就是函数 $f(x)$ 的积分。

期望法

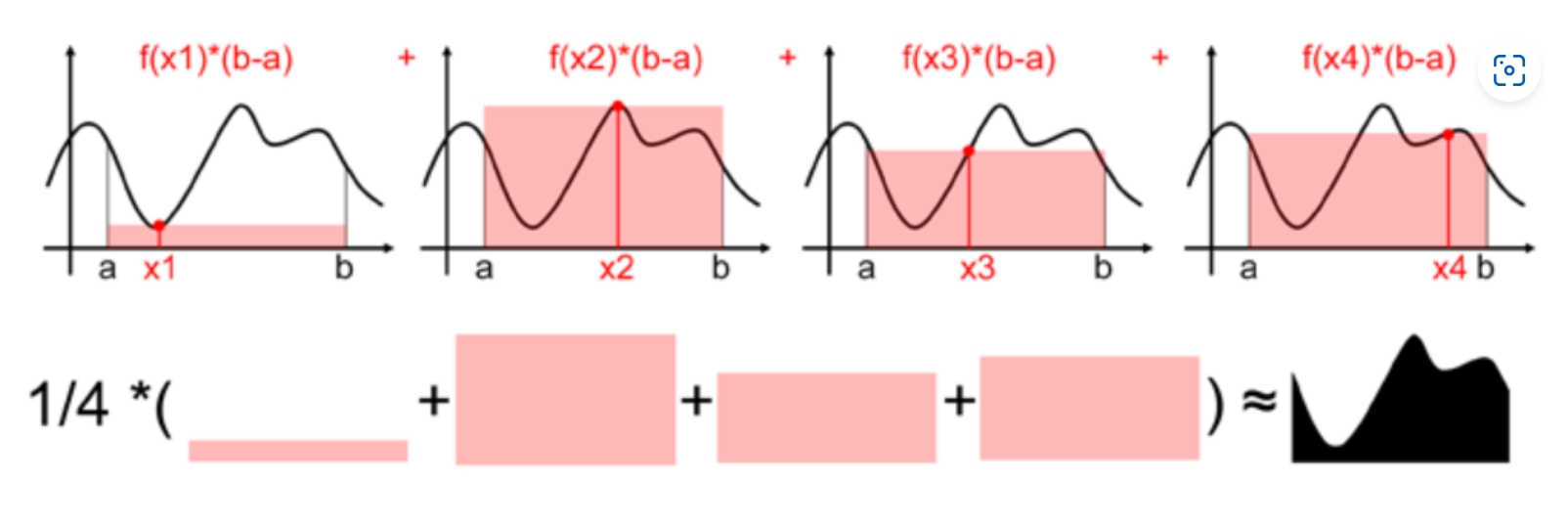
$\frac{1}{b-a}\int_a^b f(x)dx \approx \frac{1}{N}\sum_{i=1}^Nf(X_i) \\\\ \int_a^b f(x)dx \approx (b-a)\frac{1}{N}\sum_{i=1}^Nf(X_i)$

下面用蒙特卡洛期望法复现上面的二重积分的计算结果

#####using monte-carlo mean value method
points_list = [10, 100, 1000, 5000, 10000, 20000, 30000, 40000, 50000]
val = [ ]
for num_points in points_list:
    a = np.array([0, -6])
    b = np.array([np.pi, 6])
    random_samples = a + (b-a)*np.random.rand(num_points, 2)
    phi = random_samples[:,0]
    x = random_samples[:,1]
    vec_fun_real = np.vectorize(fun_real) # vectorize 并行化
    re = vec_fun_real(phi, x, 0, 0, mu_x, mu_p, sigma_x, sigma_p)
    volume = np.prod(b-a)
    integral = volume * np.mean(re)
    val.append(integral)
    print(num_points, integral)

10 0.9979157216425696
100 0.514142044598702
1000 0.7160325404556297
5000 0.6784637916809562
10000 0.6484013347494099
20000 0.633254655275164
30000 0.6674545512520975
40000 0.6440547100815087
50000 0.6630202830049494

可以看到最后结果会收敛到0.64左右。

两模线路的量子态层析

考虑两模光量子线路，算符 $H$ 的平均值如下:

$\begin{aligned} \langle H\rangle&=\int_0^\pi\int_0^\pi\frac{d\phi_1d\phi_2}{\pi^2}\int_{-\infty}^\infty\int_{-\infty}^\infty dx_1dx_2 p(\phi_1,\phi_2,x_1,x_2)K(\phi_1,\phi_2,x_1,x_2,H) \end{aligned}$

$p(\phi_1,\phi_2,x_1,x_2)$ 的定义如下:

$\begin{aligned} &p(\phi_1,\phi_2,x_1,x_2) = p(\frac{1}{2}(\cos\phi_1 x_1 + \sin\phi_1 p_1), \frac{1}{2}(\cos\phi_2 x_2 + \sin\phi_2 p_2)) = p(X_1, X_2) \\\\ &X_1 = \frac{1}{2}(\cos\phi_1 x_1 + \sin\phi_1 p_1)\\\\ &X_2 = \frac{1}{2}(\cos\phi_2 x_2 + \sin\phi_2 p_2) \end{aligned}$

对应的平均值及协方差如下：

$\begin{aligned} &\mu(X_1) = \frac{1}{2}(\cos\phi_1 \mu_{x_1} + \sin\phi_1 \mu_{p_1}) \\\\ &\mu(X_2) = \frac{1}{2}(\cos\phi_2 \mu_{x_2} + \sin\phi_2 \mu_{p_2}) \\\\ &cov(X_1, X_2) = cov(\frac{1}{2}(\cos\phi_1 x_1 + \sin\phi_1 p_1), \frac{1}{2}(\cos\phi_2 x_2 + \sin\phi_2 p_2)) = \\\\ &\frac{1}{4}(\cos\phi_1 \cos\phi_2 cov(x_1, x_2) + \cos\phi_1 \sin\phi_2 cov(x_1, p_2) + \sin\phi_1 \cos\phi_2 cov(p_1, x_2) + \sin\phi_1 \sin\phi_2 cov(p_1, p_2) \\\\ &cov(X_1, X_1) = \frac{1}{4}(\cos^2\phi_1 cov(x_1, x_1) + sin^2\phi_1 cov(p_1, p_1) + 2\cos\phi_1\sin\phi_1cov(x_1, p_1)) \\\\ &cov(X_2, X_2) = \frac{1}{4}(\cos^2\phi_2cov(x_2, x_2) + sin^2\phi_2 cov(p_2, p_2) + 2\cos\phi_2\sin\phi_2cov(x_2, p_2)) \\\\ \end{aligned}$

$K(\phi_1,\phi_2,x_1,x_2,H)$ 的定义如下

$\begin{aligned}K(\phi_{1},\phi_{2},x_{1},x_{2},H)&=\int_{-\infty}^{\infty}dr_{1}dr_{2}\Pi_{m=1}^{2}\frac{|r_{m}|}{4}Tr(He^{ir_{m}(X_{\phi_{m}}-x_{m})}) \end{aligned}$

当 $H = H_1 \otimes H_2$ 时，核函数可以简单表示成两个独立部分的乘积。

$K(\phi_1,\phi_2,x_1,x_2,H) = K(\phi_1,x_1,H_1)\cdot K(\phi_2,x_2,H_2)$

比如考虑两模算符 $H = |00\rangle\langle 00|$ ，使用下面的化简公式

令
$O_1 = (|0\rangle\langle0|)_1 \\ O_2 = (|0\rangle\langle0|)_2$
对应的核函数可以写成

$K(\phi_1,\phi_2,x_1,x_2,O) = K(\phi_1,x_1,O_1)\cdot K(\phi_2,x_2,O_2)$

下面以两模线路为例，计算 $|00\rangle \langle 00|$ 的期望值，

nmode = 2
cir = dq.QumodeCircuit(nmode=nmode, init_state='vac', cutoff=3, backend='gaussian')
cir.s(0, r=1)
cir.s(1, r=1)
cir.bs([0,1], [np.pi/4, np.pi/4])
state =cir()
probs = cir(is_prob=True)
cir.draw()

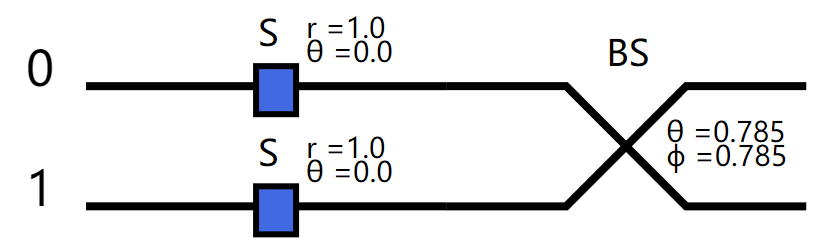
def get_mu_sigma(phi_1, phi_2, mu, sigma):
    mu_1 = 0.5*(np.cos(phi_1)*mu[0] + np.sin(phi_1)*mu[2])
    mu_2 = 0.5*(np.cos(phi_2)*mu[1] + np.sin(phi_2)*mu[3])
    cov_x1x1 = 0.25*(np.cos(phi_1)**2*sigma[0,0] + np.sin(phi_1)**2*sigma[2,2]+np.sin(2*phi_1)*sigma[0,2])
    cov_x2x2 = 0.25*(np.cos(phi_2)**2*sigma[1,1] + np.sin(phi_2)**2*sigma[3,3]+np.sin(2*phi_2)*sigma[1,3])
    cov_x1x2 = 0.25*(np.cos(phi_1)*np.cos(phi_2)*sigma[0,1] + np.cos(phi_1)*np.sin(phi_2)*sigma[0,3] + \
            np.sin(phi_1)*np.cos(phi_2)*sigma[2,1] + np.sin(phi_1)*np.sin(phi_2)*sigma[2,3])
    mu_ = np.array([mu_1, mu_2])
    sigma_ =np.array([[cov_x1x1, cov_x1x2],
                      [cov_x1x2, cov_x2x2]])
    return mu_, sigma_
def fun_twomode(phi_1, phi_2, x_1, x_2, n_1, labda_1, n_2, labda_2, mu, sigma):
    """
    calculating expectation value of operator |n_1+labda_1><n1| \otimes |n_2+labda_2><n2|
    """
    mu_, sigma_ = get_mu_sigma(phi_1, phi_2, mu, sigma)
    sigma_inv = np.linalg.inv(sigma_)
    x_ = np.array([x_1, x_2]) - mu_
    p =  1/(2*np.pi*np.sqrt(np.linalg.det(sigma_)))*np.exp(-x_.transpose()@sigma_inv@x_)
    kernel = K_A(x=x_1, phi=phi_1, n=n_1, labda=labda_1) * K_A(x=x_2, phi=phi_2, n=n_2, labda=labda_2) 

    return p * kernel/np.pi**2

一般情况下 $\mu_x, \mu_p, \sigma_x, \sigma_p, cov(x,p)$ 是通过homodyne测量结果做统计学分析得到的，这里为了方便，直接用前向计算的结果代替homodyne测量结果。同时使用蒙特卡洛方法计算对应的四重积分。

sigma_ = np.array(state[0][0])
mu_ = np.array(state[1][0].squeeze())
sigma_, mu_

(array([[ 1.948765 ,  0.       ,  1.8134297, -2.564577 ],
        [ 0.       ,  1.948765 , -2.564577 , -1.8134297],
        [ 1.8134297, -2.564577 ,  5.5756254,  0.       ],
        [-2.564577 , -1.8134297,  0.       ,  5.5756254]], dtype=float32),
 array([0., 0., 0., 0.], dtype=float32))

下面通过蒙特卡洛方法计算四重积分

def fun_real_two(phi_1, phi_2, x_1, x_2, n_1, labda_1, n_2, labda_2, mu=mu_, sigma=sigma_):
    return fun_twomode(phi_1, phi_2, x_1, x_2, n_1, labda_1, n_2, labda_2, mu, sigma).real

def fun_imag_two(phi_1, phi_2, x_1, x_2, n_1, labda_1, n_2, labda_2, mu=mu_, sigma=sigma_):
    return fun_twomode(phi_1, phi_2, x_1, x_2, n_1, labda_1, n_2, labda_2, mu, sigma).imag

num_points = int(5e4)
a1 = np.array([0, 0, -6, -6])
b1 = np.array([np.pi, np.pi, 6, 6])
random_samples = a1 + (b1-a1)*np.random.rand(num_points, 4)
phi_1 = random_samples[:,0]
phi_2 = random_samples[:,1]
x_1 = random_samples[:,2]
x_2 = random_samples[:,3]

vec_fun_real = np.vectorize(fun_real_two) # vectorize 并行化
re = vec_fun_real(phi_1, phi_2, x_1, x_2, 0, 0, 0,0)
volume = np.prod(b1-a1)
integral = volume * np.mean(re)
print(integral)

0.4254756948069217

输出理论计算的值进行对比

probs = cir(is_prob=True)
probs

{|00>: tensor([0.4200]),
 |02>: tensor([0.0609]),
 |11>: tensor([0.1218]),
 |20>: tensor([0.0609]),
 |22>: tensor([0.0088]),
 |01>: tensor([0.]),
 |10>: tensor([0.]),
 |12>: tensor([0.]),
 |21>: tensor([0.])}

附录

[1] 秦忠忠，王美红，马荣，苏晓龙. 压缩态光场及其应用研究进展[J]. 激光与电子学进展.

[2] D’Ariano G M, Maccone L, Sacchi M F. Homodyne tomography and the reconstruction of quantum states of light[M] Quantum Information With Continuous Variables of Atoms and Light. 2007: 141-158.

[3] Shang Z X, Zhong H S, Zhang Y K, et al. Boson sampling enhanced quantum chemistry[J]. arXiv preprint arXiv:2403.16698, 2024.

文档链接

案例代码