基于连续变量的光量子一维纠缠态制备

Loading

纠缠态制备

在量子比特系统和连续变量系统中量子纠缠都是量子信息的关键资源，最常用的纠缠态是EPR态 和GHZ态，它们在量子通信和量子网络中都起到了关键作用。量子光学中制备这些纠缠态的方法是通过分束器混合两束压缩光，然后产生纠缠态。然而一般的制备方法都是针对特定的纠缠态设计特定的实验架构，这些方法不具有普遍性。2019年，日本东京大学Furusawa组提出一种基于延时线圈的时域复用方法[1]，可以通过这种方法制备多种纠缠态，包括常见的EPR态 和GHZ态。自此以后研究者们通过时域复用技术构造了各种大规模一维或者二维的簇态[2,3]，向实现通用量子计算迈进一大步。这里我们以一维的EPR和GHZ态为例，详细介绍如何通过DeepQuantum模拟实现小规模簇态的构造。

EPR 和GHZ 态简单介绍

  1. 两模线路制备EPR态的图示如下:

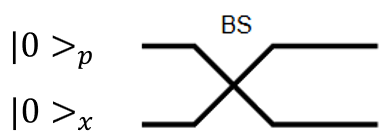
对应两模输入的量子态分别是|0\rangle_p, |0\rangle_x, 其中|0\rangle_p 可以通过傅里叶变换用x 基矢表示。

|0\rangle_p = \int_{-\infty}^{+\infty} |a\rangle_x d a

那么经过一个1:1的分束器之后量子态可以变为，

BS \int_{-\infty}^{+\infty} |a\rangle_x^A |0\rangle_x^Bd a = \int_{-\infty}^{+\infty} |\frac{a}{\sqrt{2}}\rangle_x^A |\frac{a}{\sqrt{2}}\rangle_x^Bd a \sim \int_{-\infty}^{+\infty} |x\rangle_x^A |x\rangle_x^Bd x

从最后的结果可看到当第一个模式进行Homodyne测量到x_0时， 第二个模式进行Homodyne测量同样会得到x_0。

  1. 三模线路制备GHZ态的图示如下:

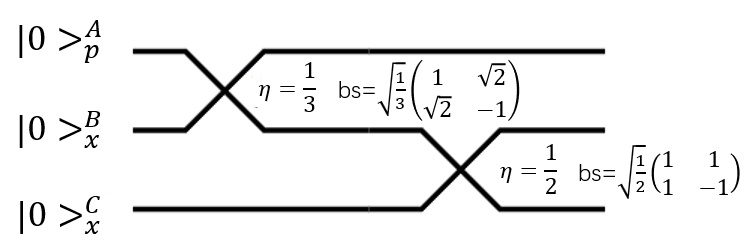
对应三模输入的量子态分别是|0\rangle_p^A, |0\rangle_x^B, |0\rangle_x^C, 其中|0\rangle_p 可以通过傅里叶变换用x 基矢表示, 初始系统的量子态如下，

\int_{-\infty}^{+\infty} |a\rangle_x^A |0\rangle_x^B |0\rangle_x^C d a

那么经过第一个1:2的分束器之后量子态可以变为，

BS_1 \int_{-\infty}^{+\infty} |a\rangle_x^A |0\rangle_x^B |0\rangle_x^C d a = \int_{-\infty}^{+\infty} |\sqrt{\frac{1}{3}}a\rangle_x^A |\sqrt{\frac{2}{3}}a\rangle_x^B|0\rangle_x^C d a

经过第二个1:1的分束器之后量子态可以变为，

\int_{-\infty}^{+\infty} |\sqrt{\frac{1}{3}}a\rangle_x^A |\sqrt{\frac{1}{3}}a\rangle_x^B|\sqrt{\frac{1}{3}}a\rangle_x^C da\sim
\int_{-\infty}^{+\infty} |x\rangle_x^A |x\rangle_x^B|x\rangle_x^C dx

从最后的结果可看到当第一个模式进行Homodyne测量到x_0时， 第二、三个模式进行Homodyne测量同样会得到x_0。

注意这里|0\rangle_p, |0\rangle_x 都是理想情况下的连续变量量子态，分别表示p方向和x方向的完美压缩态， 一般实验中会采用压缩态来近似， 通过\frac{\pi}{2}的旋转门可以实现|0\rangle_p和|0\rangle_x 的相互转换。

时域复用核心模块介绍

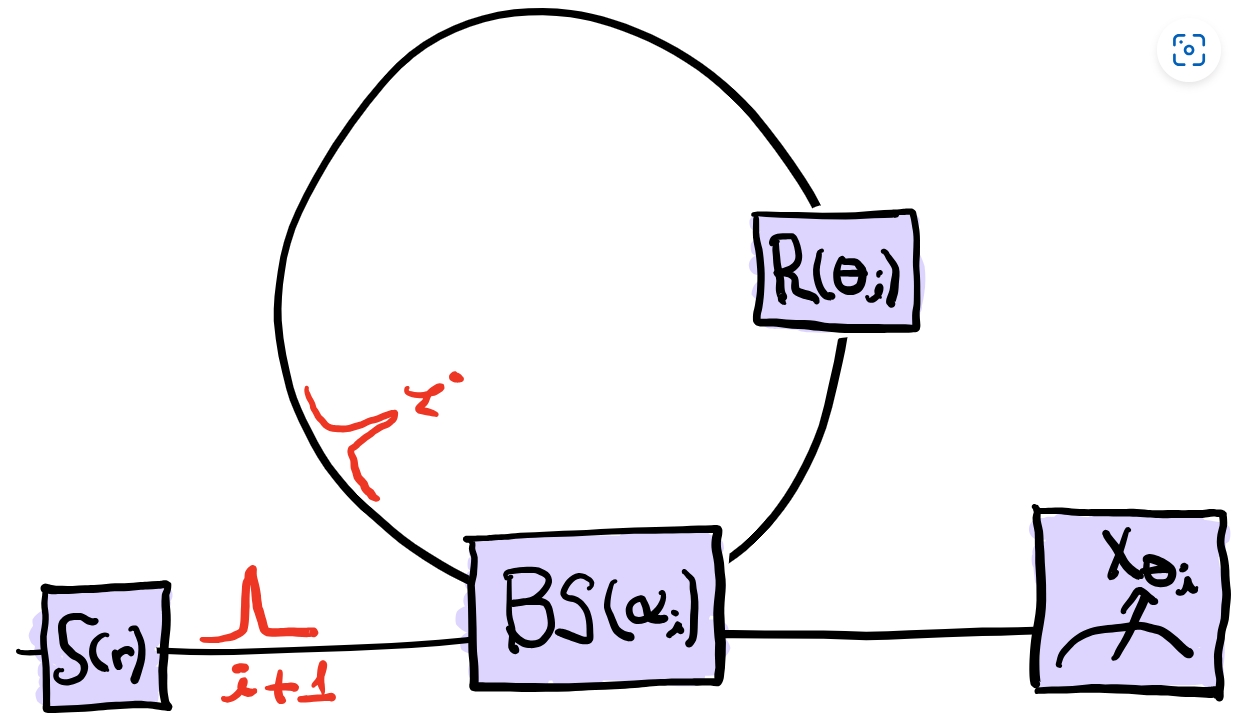
单模线路的时域复用线路结构如上图，核心模块是可调分束器+延时线圈+可调移相器结构，初始状态下延时线中是真空态，分束器角度设为\frac{\pi}{2}，输入的压缩态经过可调分束器和延时线圈中的真空态形成置换，第一次输出真空态。然后延时线圈中变为压缩态，第二次输入时域束器角度设为特定值(比如\frac{\pi}{4})，将两个压缩态纠缠起来，然后其中的一部分通过Homodyne测量探测输出，另一部分继续通过延时线圈和下一个输入的压缩态形成干涉(或者置换)，然后部分纠缠态继续输出，如此往复。通过设计可调分束器和可调移相器角度周期性变化，以及变化周期匹配输入光源频率，可以制备出多种形式的一维纠缠态，比如EPR态，GHZ态，星状纠缠态等等(见下图)。

通过时域复用模块来制备EPR态和GHZ态其实就是通过设置周期性分束器和移相器角度，使得时域复用线路可以等效1.1中的光量子线路。下面介绍如何通过时域复用线路制备EPR态和GHZ态。

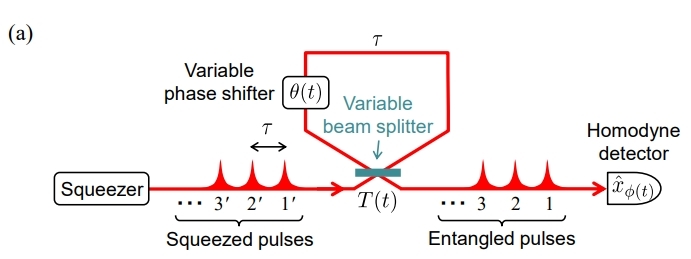
1.EPR 态的制备

分束器周期性变化角度为\frac{\pi}{2},\frac{\pi}{4}， 旋转门对应的周期性变化角度为\frac{\pi}{2}， 0。第一个X压缩态输入通过\frac{\pi}{2}的分束器置换出真空态， 然后通过\frac{\pi}{2}旋转门变换成P压缩态。 第二个X压缩态输入通过1:1分束器和P压缩态形成纠缠，然后其中一部分输出经过Homodyne 探测， 剩余部分和第三个X压缩态置换输出然后经过Homodyne探测。因此相邻两次输出的一定是EPR纠缠态， 相邻两次探测结果也是纠缠的。

2.GHZ 态的制备

分束器周期性变化角度为\frac{\pi}{2},\theta, \frac{\pi}{4} (\theta 是 1:2分束对应的角度)， 旋转门对应的周期性变化角度为\frac{\pi}{2}, 0, 0。第一个X压缩态输入通过\frac{\pi}{2}的分束器置换出真空态， 然后通过\frac{\pi}{2}旋转门变换成P压缩态。第二个X压缩态输入通过1:2分束器和P压缩态形成纠缠，然后其中一部分输出经过Homodyne 探测， 剩余部分和第三个X压缩态通过1:1分束器和P压缩态形成纠缠，然后其中一部分输出经过Homodyne 探测，剩余部分和第四个X压缩态置换输出然后经过Homodyne探测。因此相邻三次输出的一定是GHZ纠缠态， 相邻三次探测结果也是纠缠的。

代码演示

下面演示如何通过DeepQuantum时域复用模块制备简单的纠缠态。

EPR 态

import deepquantum as dq
import numpy as np
import torch

先使用QumodeCircuitTDM模块搭建单模时域复用线路，这个模块使用高斯后端。延时线圈参数 n_\tau=1，对应着延时线里只能同时存在一个量子态。周期性参数编码为 [\frac{\pi}{2}, \frac{\pi}{2}] 和 [\frac{\pi}{4}, 0]，对应着分束器周期性变化角度为 \frac{\pi}{2}、\frac{\pi}{4}，旋转门的周期性变化角度为 \frac{\pi}{2}、0。

r = 9
nmode = 1
cir = dq.QumodeCircuitTDM(nmode=nmode, init_state='vac', cutoff=3)
cir.s(0, r=r)
cir.delay(0, ntau=1, inputs=[np.pi/2, np.pi/2], encode=True) # 参数编码
cir.homodyne_x(0)
cir.draw()

完成线路前向运行之后可以查看等效的线路

cir()
cir.draw(unroll=True)

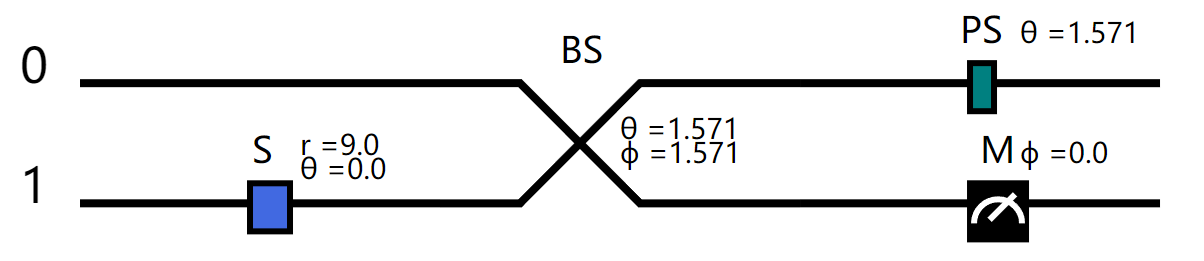
现在编码周期性参数，然后运行线路同时进行Homodyne 测量采样， 可以看到采样结果是两两关联的(第一次是真空态的采样结果)

data1 = torch.tensor([[np.pi/2, np.pi/2],
                      [np.pi/4, 0]])
data2 = data1.unsqueeze(0)
cir(data=data2, nstep=13)
sample = cir.samples
sample

tensor([ 2.6129e-01,  1.6333e+03,  1.6333e+03, -7.7196e+03, -7.7196e+03,
         6.2616e+03,  6.2616e+03, -7.2028e+03, -7.2028e+03,  1.4541e+03,
         1.4541e+03, -2.0832e+02, -2.0832e+02])

同时还支持多个batch参数的编码， 输出对应的batch结果

data3 = torch.stack([data1, data1])
cir(data=data3, nstep=13)
sample = cir.samples
sample.mT

tensor([[-3.5337e-01,  3.0907e-02],
        [-4.4619e+03, -3.6518e+03],
        [-4.4619e+03, -3.6518e+03],
        [ 4.9993e+03,  8.8810e+03],
        [ 4.9993e+03,  8.8810e+03],
        [ 6.7291e+02, -3.1233e+03],
        [ 6.7291e+02, -3.1233e+03],
        [ 2.9594e+03,  3.4443e+02],
        [ 2.9594e+03,  3.4443e+02],
        [-1.0142e+04, -4.0096e+03],
        [-1.0142e+04, -4.0096e+03],
        [-4.5157e+03,  8.4860e+03],
        [-4.5157e+03,  8.4860e+03]])

GHZ态

先使用QumodeCircuitTDM模块搭建单模时域复用线路，延时线圈参数 n_\tau=1，对应着延时线里只能同时存在一个量子态。周期性参数编码为 [\frac{\pi}{2}, \frac{\pi}{2}]、[\theta_1, 0] 和 [\theta_2, 0]，对应着分束器周期性变化角度为 \frac{\pi}{2}、\theta_1、\theta_2，旋转门的周期性变化角度为 \frac{\pi}{2}、0、0。\theta_1 和 \theta_2 对应分束器分束比为 1:2 和 1:1 的角度。

r = 6
nmode = 1
theta1 = torch.arcsin(torch.sqrt(torch.tensor(1/3)))
theta2 = torch.arcsin(torch.sqrt(torch.tensor(1/2)))
cir = dq.QumodeCircuitTDM(nmode=nmode, init_state='vac', cutoff=3)
cir.s(0, r=r)
cir.delay(0, ntau=1, inputs=[np.pi/2, np.pi/2], encode=True)
cir.homodyne_x(0)
cir.draw()


cir()
cir.draw(unroll=True)

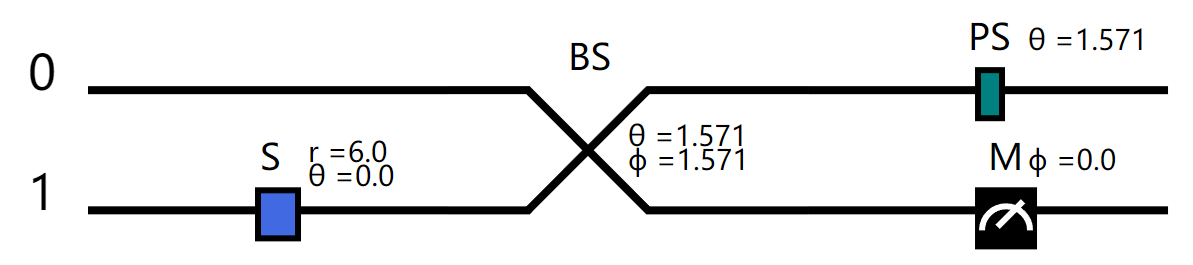
现在编码周期性参数，然后运行线路同时进行Homodyne 测量采样， 可以看到相邻的三个采样结果是关联的(第一次采样是真空态的采样结果)。

data1 = torch.tensor([[np.pi/2, np.pi/2],
                      [theta1, 0],
                      [theta2, 0]])
data2 = data1.unsqueeze(0)
cir(data=data2, nstep=13)
samples = cir.samples
samples

tensor([   0.9922,  204.2620,  204.2588,  204.2644, -193.9315, -193.9335,
        -193.9291,  112.1219,  112.1223,  112.1217,  160.9689,  160.9710,
         160.9668])

同时还支持多个batch参数的编码， 输出对应的batch结果。

data3 = torch.stack([data1, data1])
cir(data=data3, nstep=14)
samples = cir.samples
samples.mT

tensor([[ 9.6568e-01,  3.3229e-01],
        [-3.4941e+01,  1.7617e+01],
        [-3.4941e+01,  1.7615e+01],
        [-3.4940e+01,  1.7618e+01],
        [ 3.3926e+02,  4.2417e+02],
        [ 3.3926e+02,  4.2417e+02],
        [ 3.3926e+02,  4.2417e+02],
        [ 8.1260e+01,  6.1261e+01],
        [ 8.1259e+01,  6.1259e+01],
        [ 8.1261e+01,  6.1262e+01],
        [ 2.4085e+02, -1.1090e+02],
        [ 2.4084e+02, -1.1090e+02],
        [ 2.4085e+02, -1.1090e+02],
        [ 8.2308e+01, -1.6484e+02]])

附录

[1] Takeda S, Takase K, Furusawa A. On-demand photonic entanglement synthesizer[J]. Science advances, 2019, 5(5): eaaw4530.

[2] Yokoyama S, Ukai R, Armstrong S C, et al. Ultra-large-scale continuous-variable cluster states multiplexed in the time domain[J]. Nature Photonics, 2013, 7(12): 982-986.

[3] Asavanant W. Time-Domain Multiplexed 2-Dimensional Cluster State: Universal Quantum Computing Platform[J]. arxiv. org, Cornell University Library, 201.

文档链接

案例代码

图灵算法

图灵算法

图灵算法组是一个神秘的算法组织。他们的工作是研究神秘的量子算法。感谢杨杰诚提供的29个算法案例；感谢胡克明提供的10个算法案例；感谢朱宇泽提供的2个算法案例；感谢张者勇提供的2个算法案例；感谢何俊杰提供的1个算法案例；感谢李瑞琦提供的1个算法案例。